《2025年名师帮同步学案九年级数学全一册人教版》

1. 如图,在平面直角坐标系中,$△ABC$三个顶点的坐标分别为$A(1,-1)$,$B(2,-5)$,$C(5,-4)$.
(1)画出与$△ABC$关于原点$O$对称的$△A_{1}B_{1}C_{1}$;
(2)画出将$△A_{1}B_{1}C_{1}$绕原点$O$顺时针旋转$90^{\circ}$后得到的$△A_{2}B_{2}C_{2}$,写出点$B_{2}$的坐标;
(3)试说明$△ABC$经过怎样的变换可以得到$△A_{2}B_{2}C_{2}$.

答案：
解:
(1) 如图所示, $\triangle A_1 B_1 C_1$ 即为所求;
　
(2) 如图所示, $\triangle A_2 B_2 C_2$ 即为所求,
　
点 $B_2$ 的坐标为 $(5,2)$;
(3) 将 $\triangle A B C$ 绕原点 $O$ 逆时针旋转 $90^{\circ}$ 后可以得到 $\triangle A_2 B_2 C_2$.

2. 如图,把正方形$ABCD$绕点$C$按顺时针方向旋转$45^{\circ}$得到正方形$A'B'CD'$(此时,点$B'$落在对角线$AC$上,点$A'$落在$CD$的延长线上),$A'B'$交$AD$于点$E$,连接$AA'$,$CE$. 求证:$△ADA'\cong △CDE$.

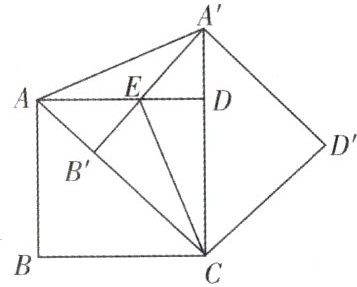
证明: $\because$ 四边形 $A B C D$ 是正方形,
$\therefore A D=CD, \angle A D C=90^{\circ}$,
$\therefore \angle A^{\prime} D A=90^{\circ}$,
根据旋转的方法可得 $\angle E A^{\prime} D=45^{\circ}$,
$\therefore \angle A^{\prime} E D=45^{\circ}, \therefore A^{\prime} D=D E$,
在 $\triangle A A^{\prime} D$ 和 $\triangle C E D$ 中,
$\left\{\begin{array}{l}A D=C D, \\ \angle A D A^{\prime}=\angle C D E, \\ A^{\prime} D=E D,\end{array}\right.$
$\therefore \triangle A D A^{\prime} \cong \triangle C D E$(SAS).

答案： 证明: $\because$ 四边形 $A B C D$ 是正方形,
$\therefore A D=C D, \angle A D C=90^{\circ}$,
$\therefore \angle A^{\prime} D A=90^{\circ}$,
根据旋转的方法可得 $\angle E A^{\prime} D=45^{\circ}$,
$\therefore \angle A^{\prime} E D=45^{\circ}, \therefore A^{\prime} D=D E$,
在 $\triangle A A^{\prime} D$ 和 $\triangle C E D$ 中,
$\left\{\begin{array}{l}A D=C D, \\ \angle A D A^{\prime}=\angle C D E, \\ A^{\prime} D=E D,\end{array}\right.$
$\therefore \triangle A D A^{\prime} \cong \triangle C D E(S A S)$.

3. (2025·绵阳一模)已知点$N$是菱形$ABCD$边$AD$的中点,将菱形$ABCD$绕点$N$逆时针旋转得到菱形$EFGH$,使点$A$的对应点$E$落在线段$AB$上,边$EF$经过点$D$.
(1)求证:$DE⊥AB$;
(2)若$DF=\sqrt{2}-1$,求$CD$的长.$\sqrt{2}$

答案：
(1) 证明: $\because$ 四边形 $A B C D$ 是菱形,
$\therefore A B=B C=C D=D A$,
$\because$ 点 $N$ 是 $A D$ 的中点,
$\therefore A N=N D$,
由旋转可知 $N A=N E=N D$,
$\therefore \angle A=\angle A E N, \angle A D E=\angle D E N$,
又 $\because \angle A+\angle A E N+\angle A D E+\angle D E N=180^{\circ}$,
$\therefore 2 \angle A E N+2 \angle D E N=180^{\circ}$,
$\therefore \angle A E N+\angle D E N=90^{\circ}$,
$\therefore D E \perp A B$;
(2) 解: 由旋转可知 $\angle A=\angle D E N$,
$\therefore \angle A=\angle A E N=\angle A D E=\angle D E N$,
$\because \angle A+\angle A E N+\angle A D E+\angle D E N=180^{\circ}$,
$\therefore \angle A=\angle A E N=\angle A D E=\angle D E N=45^{\circ}$,
$\therefore E A=E D$,
又 $\because A B=E F$,
$\therefore B E=D F=\sqrt{2}-1$,
设 $A E=D E=x$, 在 $\mathrm{Rt} \triangle A D E$ 中,
$A D=\sqrt{A E^2+D E^2}=\sqrt{2} x$,
$\therefore A B=A D=\sqrt{2} x$,
$\therefore B E=\sqrt{2} x-x=\sqrt{2}-1$,
$\therefore x=1$,
$\therefore C D=A B=\sqrt{2} x=\sqrt{2}$,
$\therefore C D$ 的长为 $\sqrt{2}$.