第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
垂径定理:垂直于弦的直径
平分
这条弦,并且平分
弦所对的两条弧.
答案:
平分 平分
1. 如图,$AB$是$\odot$的直径,弦$CD\perp AB$,垂足为$M$,下列结论不成立的是 (
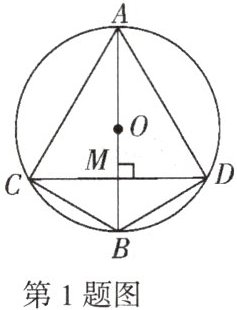
A. $CM = DM$
B. $\overset{\frown}{CB}=\overset{\frown}{DB}$
C. $\angle ACD=\angle ADC$
D. $OM = MD$
D
)
A. $CM = DM$
B. $\overset{\frown}{CB}=\overset{\frown}{DB}$
C. $\angle ACD=\angle ADC$
D. $OM = MD$
答案:
1. D
2. 如图,$\odot O$的半径为4,弦心距$OC = 2$,则弦$AB$的长为 (
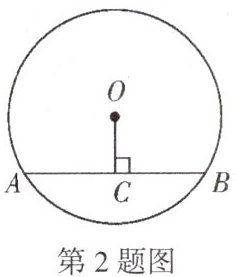
A. 3
B. $2\sqrt{3}$
C. 6
D. $4\sqrt{3}$
D
)
A. 3
B. $2\sqrt{3}$
C. 6
D. $4\sqrt{3}$
答案:
2. D
3. 如图,$AB$是$\odot O$的弦,$OC\perp AB$于$C$,若$AB = 2\sqrt{3}\text{ cm}$,$OC = 1\text{ cm}$,则$\odot O$的半径为______
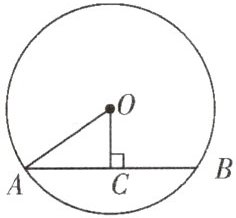
2 cm
.
答案:
3. 2 cm 解析:
∵AB是⊙O的弦,OC⊥AB于点C,
∴AC=BC=$\sqrt{3}$cm。在Rt△AOC中,AO=$\sqrt{AC^{2}+OC^{2}}=\sqrt{(\sqrt{3})^{2}+1^{2}}=2$cm。
∴圆的半径为2 cm。
∵AB是⊙O的弦,OC⊥AB于点C,
∴AC=BC=$\sqrt{3}$cm。在Rt△AOC中,AO=$\sqrt{AC^{2}+OC^{2}}=\sqrt{(\sqrt{3})^{2}+1^{2}}=2$cm。
∴圆的半径为2 cm。
4. 如图,$AB$为$\odot O$的直径,弦$CD\perp AB$于$E$,已知$CD = 12$,$EB = 2$,求$\odot O$的直径.
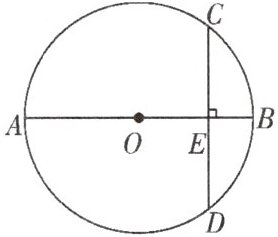
20

答案:
4. 解:连接OC,由垂径定理得CE=$\frac{1}{2}$CD=$\frac{1}{2}×12=6$,
设⊙O的半径为r,在Rt△OCE中,OE=OB - EB=r - 2,
$r^{2}=6^{2}+(r - 2)^{2}$,解得r=10,
∴⊙O的直径=2r=20。
设⊙O的半径为r,在Rt△OCE中,OE=OB - EB=r - 2,
$r^{2}=6^{2}+(r - 2)^{2}$,解得r=10,
∴⊙O的直径=2r=20。
5. 如图,在半径为$5\text{ cm}$的$\odot O$中,弦$AB = 6\text{ cm}$,$OC\perp AB$于点$C$,则$OC =$
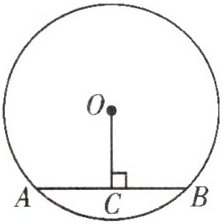
4 cm
.
答案:
5. 4 cm
6. 如图,$AB$为$\odot O$的直径,弦$CD\perp AB$于点$E$,若$AB = 26$,$EB = 8$,求弦$CD$的长.


答案:
6. 解:如图,连接OC。

∵AB是直径且AB=26,
∴OC=$\frac{1}{2}$AB=13。
又
∵BE=8,
∴OE=13 - 8=5。
又
∵CD⊥AB,
∴在Rt△OCE中,
CE=$\sqrt{OC^{2}-OE^{2}}=12$。
∴CD=2CE=24。
∴弦CD的长为24。
6. 解:如图,连接OC。

∵AB是直径且AB=26,
∴OC=$\frac{1}{2}$AB=13。
又
∵BE=8,
∴OE=13 - 8=5。
又
∵CD⊥AB,
∴在Rt△OCE中,
CE=$\sqrt{OC^{2}-OE^{2}}=12$。
∴CD=2CE=24。
∴弦CD的长为24。
查看更多完整答案,请扫码查看


