《2025年名师帮同步学案九年级数学全一册人教版》

1. 垂径定理的推论:
推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
2. 垂径定理应用中常作的辅助线:
①若已知圆心和弦,则连接圆心和弦的一个端点,即"连半径",并作垂直于弦的直径,构造直角三角形;
②若已知圆心和弦(弧)的中点,则连接圆心和弦(弧)的中点,并延长使其与圆相交,得圆的直径,再"连半径",构造直角三角形.

答案： 1.平分　圆心　平分　垂直平分

1. 如图,AB是⊙O的直径,弦CD被直径AB平分.若CD=8,OE=3,则AE的长为 (C)

A. 5
B. 6
C. 8
D. 10

答案： 1.C

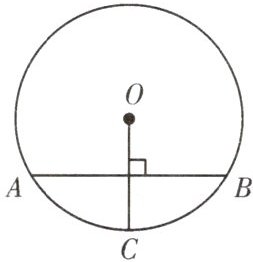
2. 在半径为13dm的圆柱形油罐内装进一些油后,横截面如图.若油面宽AB=24dm,则油的最大深度为______8dm.

答案： 2.8dm

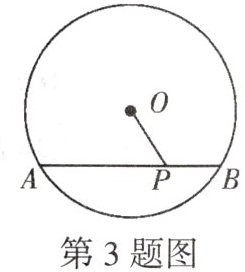
3. 如图,⊙O的直径为10,弦AB=8,点P是弦AB上一动点,那么OP长的取值范围是3≤OP≤5.

答案： 3.3≤OP≤5

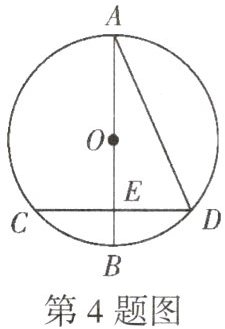
4. 如图,AB是⊙O的直径,弦CD与AB相交于点E,连接AD, $\overset{\frown}{BC}=\overset{\frown}{BD}$.若AB=10,CD=8,则AD的长为4$\sqrt{5}$.

答案： 4.4$\sqrt{5}$

5. 如图,在⊙O中,半径OC=2,弦AB垂直平分OC,求AB的长.

答案：
5.解:如图,连接OA,设OC交AB于点D.
　　　　　　
∵弦AB垂直平分OC，
∴OD=CD=$\frac{1}{2}$OC=1.
　在Rt△AOD中,AD= $\sqrt{2^2 - 1^2}$=$\sqrt{3}$;
∵OD⊥AB,
∴AD=BD=$\sqrt{3}$.
∴AB=2AD=2$\sqrt{3}$;
∴AB的长为2$\sqrt{3}$