第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. (2024·恩施校级模拟)下列式子中,不能用平方差公式运算的是 (
A. $(2-a)(-a-2)$
B. $(3x+2y)(2y-3x)$
C. $(4m-2n)(4m+2n)$
D. $(x-3)(3-x)$
D
)A. $(2-a)(-a-2)$
B. $(3x+2y)(2y-3x)$
C. $(4m-2n)(4m+2n)$
D. $(x-3)(3-x)$
答案:
D
2. (2024·南京中考)任意两个奇数的平方差总能 (
A. 被3整除
B. 被5整除
C. 被6整除
D. 被8整除
D
)A. 被3整除
B. 被5整除
C. 被6整除
D. 被8整除
答案:
D
3. 若$m+98^{2}-1= 102^{2}$,则m的值为 (
A. 100
B. 799
C. 800
D. 801
D
)A. 100
B. 799
C. 800
D. 801
答案:
D
4. (1)(2024·上海中考)计算:$(a+b)(b-a)=$
(2) 化简$x^{2}-(x+2)(x-2)$的结果是
$b^{2}-a^{2}$
;(2) 化简$x^{2}-(x+2)(x-2)$的结果是
4
.
答案:
(1) $ b^{2}-a^{2} $
(2) 4
(1) $ b^{2}-a^{2} $
(2) 4
5. 计算:(1)$(a+\frac {1}{2})(a-\frac {1}{2})=$
$a^{2}-\frac{1}{4}$
; (2)$(-x-2y)(2y-x)=$$x^{2}-4 y^{2}$
.
答案:
(1) $ a^{2}-\frac{1}{4} $
(2) $ x^{2}-4 y^{2} $
(1) $ a^{2}-\frac{1}{4} $
(2) $ x^{2}-4 y^{2} $
6. (1)$(5m-3n)$(
5m+3n
)$=25m^{2}-9n^{2}$; (2)$(-3x+2y)$(3x+2y
)$=-9x^{2}+4y^{2}$.
答案:
(1) $ 5 m+3 n $
(2) $ 3 x+2 y $
(1) $ 5 m+3 n $
(2) $ 3 x+2 y $
7. 已知$x^{2}-y^{2}= 20,x+y= 4$,则$x-y$的值是
5
.
答案:
5
8. 计算:
(1)$(2a-\frac {1}{4})(2a+\frac {1}{4})$;
(2)$(1-x)(x+1)$;
(3)$(\frac {1}{2}a+\frac {1}{4}b)(\frac {1}{4}b-\frac {1}{2}a)$;
(4)$(-ab+\frac {1}{4})(-ab-\frac {1}{4})$.
(1)$(2a-\frac {1}{4})(2a+\frac {1}{4})$;
(2)$(1-x)(x+1)$;
(3)$(\frac {1}{2}a+\frac {1}{4}b)(\frac {1}{4}b-\frac {1}{2}a)$;
(4)$(-ab+\frac {1}{4})(-ab-\frac {1}{4})$.
答案:
1. (1)
解:根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,对于$(2a-\frac{1}{4})(2a+\frac{1}{4})$,这里$m = 2a$,$n=\frac{1}{4}$。
则$(2a-\frac{1}{4})(2a+\frac{1}{4})=(2a)^{2}-(\frac{1}{4})^{2}=4a^{2}-\frac{1}{16}$。
2. (2)
解:$(1 - x)(x + 1)=(1 - x)(1 + x)$,根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m = 1$,$n=x$。
则$(1 - x)(1 + x)=1^{2}-x^{2}=1 - x^{2}$。
3. (3)
解:$(\frac{1}{2}a+\frac{1}{4}b)(\frac{1}{4}b-\frac{1}{2}a)=(\frac{1}{4}b+\frac{1}{2}a)(\frac{1}{4}b-\frac{1}{2}a)$,根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=\frac{1}{4}b$,$n = \frac{1}{2}a$。
则$(\frac{1}{4}b+\frac{1}{2}a)(\frac{1}{4}b-\frac{1}{2}a)=(\frac{1}{4}b)^{2}-(\frac{1}{2}a)^{2}=\frac{1}{16}b^{2}-\frac{1}{4}a^{2}$。
4. (4)
解:$(-ab+\frac{1}{4})(-ab-\frac{1}{4})=(-ab)^{2}-(\frac{1}{4})^{2}$(根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=-ab$,$n = \frac{1}{4}$)。
因为$(-ab)^{2}=a^{2}b^{2}$,所以$(-ab+\frac{1}{4})(-ab-\frac{1}{4})=a^{2}b^{2}-\frac{1}{16}$。
综上,(1)$4a^{2}-\frac{1}{16}$;(2)$1 - x^{2}$;(3)$\frac{1}{16}b^{2}-\frac{1}{4}a^{2}$;(4)$a^{2}b^{2}-\frac{1}{16}$。
解:根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,对于$(2a-\frac{1}{4})(2a+\frac{1}{4})$,这里$m = 2a$,$n=\frac{1}{4}$。
则$(2a-\frac{1}{4})(2a+\frac{1}{4})=(2a)^{2}-(\frac{1}{4})^{2}=4a^{2}-\frac{1}{16}$。
2. (2)
解:$(1 - x)(x + 1)=(1 - x)(1 + x)$,根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m = 1$,$n=x$。
则$(1 - x)(1 + x)=1^{2}-x^{2}=1 - x^{2}$。
3. (3)
解:$(\frac{1}{2}a+\frac{1}{4}b)(\frac{1}{4}b-\frac{1}{2}a)=(\frac{1}{4}b+\frac{1}{2}a)(\frac{1}{4}b-\frac{1}{2}a)$,根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=\frac{1}{4}b$,$n = \frac{1}{2}a$。
则$(\frac{1}{4}b+\frac{1}{2}a)(\frac{1}{4}b-\frac{1}{2}a)=(\frac{1}{4}b)^{2}-(\frac{1}{2}a)^{2}=\frac{1}{16}b^{2}-\frac{1}{4}a^{2}$。
4. (4)
解:$(-ab+\frac{1}{4})(-ab-\frac{1}{4})=(-ab)^{2}-(\frac{1}{4})^{2}$(根据平方差公式$(m - n)(m + n)=m^{2}-n^{2}$,这里$m=-ab$,$n = \frac{1}{4}$)。
因为$(-ab)^{2}=a^{2}b^{2}$,所以$(-ab+\frac{1}{4})(-ab-\frac{1}{4})=a^{2}b^{2}-\frac{1}{16}$。
综上,(1)$4a^{2}-\frac{1}{16}$;(2)$1 - x^{2}$;(3)$\frac{1}{16}b^{2}-\frac{1}{4}a^{2}$;(4)$a^{2}b^{2}-\frac{1}{16}$。
9. 下列运算正确的是 (
A. $a^{6}÷a^{2}= a^{3}$
B. $3a-2a= 1$
C. $(2a-1)(2a+1)= 4a^{2}-1$
D. $(-2a)^{3}= -6a^{3}$
C
)A. $a^{6}÷a^{2}= a^{3}$
B. $3a-2a= 1$
C. $(2a-1)(2a+1)= 4a^{2}-1$
D. $(-2a)^{3}= -6a^{3}$
答案:
C
10. 如图,大正方形与小正方形的面积之差是48,则阴影部分的面积是 (
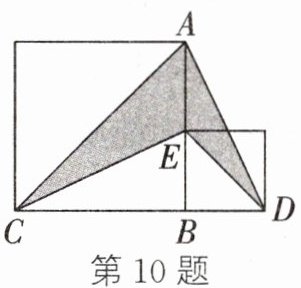
A. 12
B. 18
C. 24
D. 30
C
)
A. 12
B. 18
C. 24
D. 30
答案:
C
11. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形,分别计算这两个图形的阴影部分的面积,验证了公式
$ a^{2}-b^{2}=(a+b)(a-b) $
.
答案:
$ a^{2}-b^{2}=(a+b)(a-b) $
12. 观察下列各式的规律:
$(a-b)(a+b)= a^{2}-b^{2}$;
$(a-b)(a^{2}+ab+b^{2})= a^{3}-b^{3}$;
$(a-b)(a^{3}+a^{2}b+ab^{2}+b^{3})= a^{4}-b^{4}$;
…
可得到$(a-b)(a^{2023}+a^{2022}b+... +ab^{2022}+b^{2023})= $
$(a-b)(a+b)= a^{2}-b^{2}$;
$(a-b)(a^{2}+ab+b^{2})= a^{3}-b^{3}$;
$(a-b)(a^{3}+a^{2}b+ab^{2}+b^{3})= a^{4}-b^{4}$;
…
可得到$(a-b)(a^{2023}+a^{2022}b+... +ab^{2022}+b^{2023})= $
$a^{2024}-b^{2024}$
.
答案:
$ a^{2024}-b^{2024} $
查看更多完整答案,请扫码查看


