第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
4. 如图,$∠A= 50^{\circ },BP平分∠ABC,DP平分∠ADC,∠P= 20^{\circ }$,则$∠C$的度数为 (
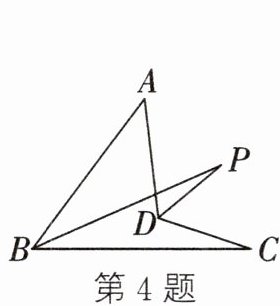
A.$20^{\circ }$
B.$15^{\circ }$
C.$5^{\circ }$
D.$10^{\circ }$
D
)
A.$20^{\circ }$
B.$15^{\circ }$
C.$5^{\circ }$
D.$10^{\circ }$
答案:
D
5. 在$△ABC$中,$∠ABC和∠ACB$的平分线交于点 O,$∠ACB的外角平分线所在直线与∠ABC$的平分线交于点 D,与$∠ABC$的外角平分线交于点 E,有下列结论:①$∠BOC= 90^{\circ }+\frac {1}{2}∠A$;②$∠D= \frac {1}{2}∠A$;③$∠E= ∠A$;④$∠E+∠DCF= 90^{\circ }+∠ABD$.其中,一定正确的是____
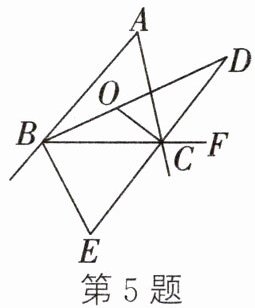
①②④
(填写所有正确结论的序号).
答案:
①②④
6. 如图,BF 平分$∠ABD$,CE 平分$∠ACD$,BF 与 CE 交于点 G.若$∠BDC= m^{\circ },∠BGC= n^{\circ }$,则$∠A$的度数为
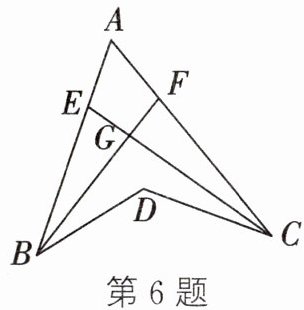
2n° - m°
(用含 m、n 的代数式表示).
答案:
2n° - m°
7. 如图,点 D、C、G 在同一直线上,BE 平分$∠ABD$交 AC 于点 E,CF 平分$∠ACG$,BE 的延长线与 CF 相交于点 F.若$∠BDC= 160^{\circ },∠A= 100^{\circ }$,则$∠F= $

40
$^{\circ }$.
答案:
40
8. (2024 秋·平顶山期末)如图,点 C、D 分别在射线 OA、OB 上,CE 是$∠ACD$的平分线,CE的反向延长线与$∠ODC$的平分线交于点 P.
(1) 如图①,当$∠AOB= ∠OCD= 60^{\circ }$时,$∠P=$
(2) 如图②,当$∠AOB= 60^{\circ }$,点 C、D 在射线 OA、OB 上任意移动时(不与点 O 重合),$∠P$的大小是否变化? 若变化,请说明理由;若不变,请求出$∠P$的度数;
(3) 如图③,若$∠OCD+∠ODC= α(0^{\circ }<α<180^{\circ })$,请直接写出$∠P$的度数(用含α的式子表示).
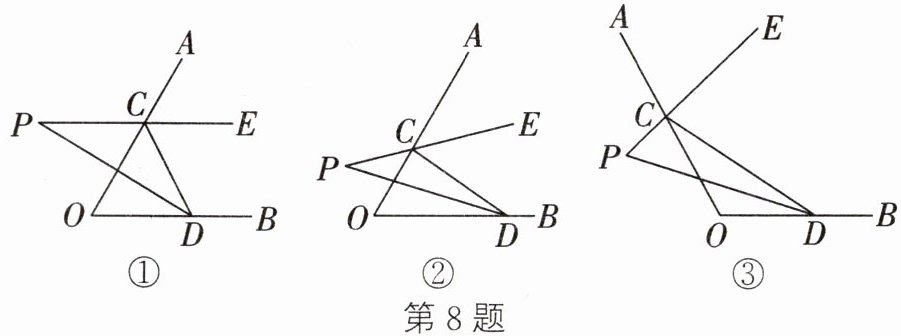
(1) 如图①,当$∠AOB= ∠OCD= 60^{\circ }$时,$∠P=$
30°
;(2) 如图②,当$∠AOB= 60^{\circ }$,点 C、D 在射线 OA、OB 上任意移动时(不与点 O 重合),$∠P$的大小是否变化? 若变化,请说明理由;若不变,请求出$∠P$的度数;
(3) 如图③,若$∠OCD+∠ODC= α(0^{\circ }<α<180^{\circ })$,请直接写出$∠P$的度数(用含α的式子表示).
90° - $\frac{1}{2}$α

答案:
解:
(1)30°
(2)∠P的大小不变,∠P = 30°,理由如下:
∵CE平分∠ACD,DP平分∠ODC,
∴∠ECD = $\frac{1}{2}$∠ACD,∠PDC = $\frac{1}{2}$∠ODC.
∴$\frac{1}{2}$∠ACD = ∠P + $\frac{1}{2}$∠ODC.
∴$\frac{1}{2}$∠ACD = $\frac{1}{2}$∠AOB + $\frac{1}{2}$∠ODC.
∴∠P = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×60° = 30°;
(3)若∠OCD + ∠ODC = α,则∠AOB = 180° - (∠OCD + ∠ODC) = 180° - α,由
(2)可得:∠P = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×(180° - α) = 90° - $\frac{1}{2}$α.
(1)30°
(2)∠P的大小不变,∠P = 30°,理由如下:
∵CE平分∠ACD,DP平分∠ODC,
∴∠ECD = $\frac{1}{2}$∠ACD,∠PDC = $\frac{1}{2}$∠ODC.
∴$\frac{1}{2}$∠ACD = ∠P + $\frac{1}{2}$∠ODC.
∴$\frac{1}{2}$∠ACD = $\frac{1}{2}$∠AOB + $\frac{1}{2}$∠ODC.
∴∠P = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×60° = 30°;
(3)若∠OCD + ∠ODC = α,则∠AOB = 180° - (∠OCD + ∠ODC) = 180° - α,由
(2)可得:∠P = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×(180° - α) = 90° - $\frac{1}{2}$α.
查看更多完整答案,请扫码查看


