第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. (2024·常州一模)王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的 (
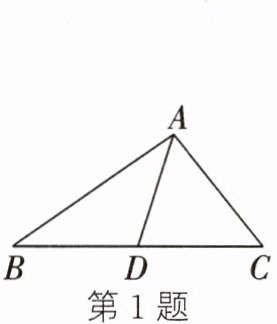
A. 角平分线
B. 中线
C. 高线
D. 以上都不是
B
)
A. 角平分线
B. 中线
C. 高线
D. 以上都不是
答案:
B
2. (2025·郑州模拟)如图,线段DG、EM、FN两两相交于B、C、A三点,则∠D+∠E+∠F+∠G+∠M+∠N的度数是 (
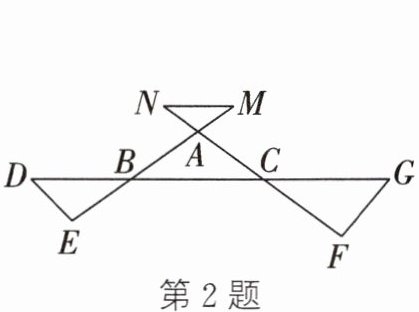
A. 180°
B. 360°
C. 540°
D. 720°
B
)
A. 180°
B. 360°
C. 540°
D. 720°
答案:
B
3. 如图,在△ABC中,AB= 18,AC= 15,AD为中线,则△ABD与△ACD的周长之差等于______
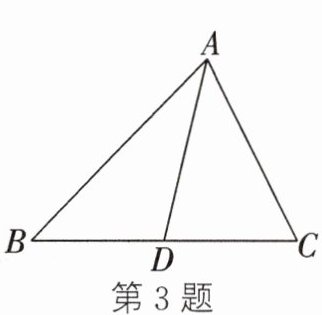
3
.
答案:
3
4. 如图,在Rt△ABC中,∠ACB= 90°,∠A= 55°,将其折叠,使点A落在边CB上的点A'处,折痕为CD,则∠A'DB= ______
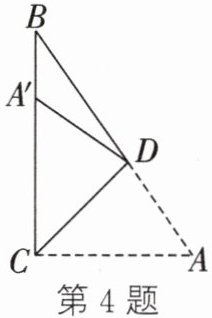
20°
.
答案:
20°
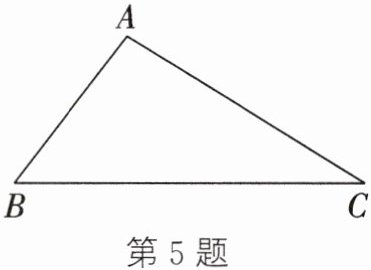
5. 如图,在△ABC中,∠BAC是钝角.
(1) 画出∠BAC的平分线AD,交BC于点D;
(2) 画出AC边上的中线BE;
(3) 画出AB边上的高CF.
(1) 画出∠BAC的平分线AD,交BC于点D;
按照上述方法可画出∠BAC的平分线AD
(2) 画出AC边上的中线BE;
按照上述方法可画出AC边上的中线BE
(3) 画出AB边上的高CF.
按照上述方法可画出AB边上的高CF(具体图形需根据上述步骤实际绘制)

答案:
按照上述方法可分别画出$\angle BAC$的平分线$AD$、$AC$边上的中线$BE$、$AB$边上的高$CF$。(具体图形需根据上述步骤实际绘制)
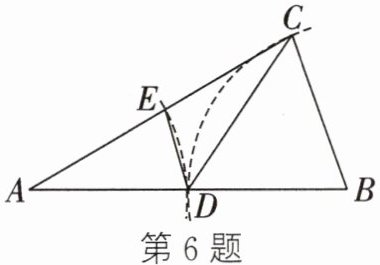
6. (2024·温州二模)尺规作图源于古希腊的数学课题,蕴含着丰富的几何原理. 如图,在△ABC中,按如下步骤尺规作图:①以点B为圆心,BC为半径作弧交边AB于点D;②以点A为圆心,AD为半径作弧交AC于点E;③连接CD与DE. 若要求∠CDE的度数,则只需知道 (
A. ∠A的度数
B. ∠B的度数
C. ∠ACB的度数
D. ∠DCE的度数
C
)
A. ∠A的度数
B. ∠B的度数
C. ∠ACB的度数
D. ∠DCE的度数
答案:
C
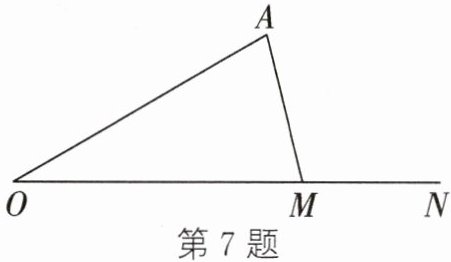
7. 如图,点M是射线ON上的一个动点(不与点O重合),点A在射线ON外,且∠AON= 30°,在点M运动过程中,若△AOM为锐角三角形,则∠A的取值范围是 (
A. 60°<∠A<90°
B. 30°<∠A<60°
C. 0°<∠A<30°
D. 0°<∠A<90°
A
)
A. 60°<∠A<90°
B. 30°<∠A<60°
C. 0°<∠A<30°
D. 0°<∠A<90°
答案:
A
查看更多完整答案,请扫码查看


