《2025年轻松作业本八年级数学上册人教版》

6. (2024·内江中考)如图,点A、D、B、E在同一条直线上,AD= BE,AC= DF,BC= EF.
(1)求证：△ABC≌△DEF；
证明：$∵ AD = BE$，$∴ AD + BD = BE + BD$，即$AB = DE$。在$△ABC$和$△DEF$中，$\begin{cases}AB = DE \\ AC = DF \\ BC = EF \end{cases}$，$∴ △ABC ≌ △DEF$(SSS)；
(2)若∠A= 55°,∠E= 45°,求∠F的度数.
解：$∵ ∠A = 55^{\circ}$，$∠E = 45^{\circ}$，由(1)可知：$△ABC ≌ △DEF$，$∴ ∠A = ∠FDE = 55^{\circ}$。$∴ ∠F = 180^{\circ} - (∠FDE + ∠E) = 180^{\circ} - (55^{\circ} + 45^{\circ}) = $80°。

答案：
(1) 证明：$∵ AD = BE$，$∴ AD + BD = BE + BD$，即$AB = DE$。在$△ABC$和$△DEF$中，$\begin{cases}AB = DE \\ AC = DF \\ BC = EF \end{cases}$，$∴ △ABC ≌ △DEF (SSS)$；
(2) 解：$∵ ∠A = 55^{\circ}$，$∠E = 45^{\circ}$，由
(1)可知：$△ABC ≌ △DEF$，$∴ ∠A = ∠FDE = 55^{\circ}$。$∴ ∠F = 180^{\circ} - (∠FDE + ∠E) = 180^{\circ} - (55^{\circ} + 45^{\circ}) = 80^{\circ}$。

7. (1)如图①,CE与AB交于点E,AC= BC,∠1= ∠2. 求证：△ACE≌△BCE；
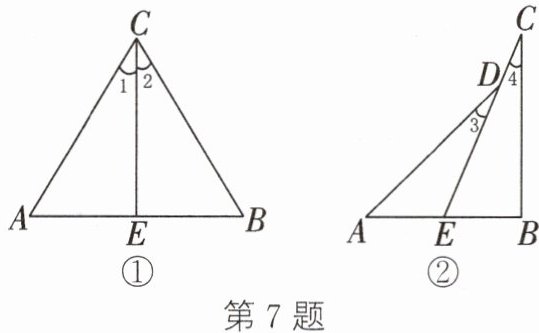
(2)如图②,CD的延长线与AB交于点E,AD= BC,∠3= ∠4. 探究AE与BE的数量关系,并说明理由.

答案：

(1) 证明：在$△ACE$和$△BCE$中，$\begin{cases}AC = BC \\ ∠1 = ∠2 \\ CE = CE \end{cases}$，$∴ △ACE ≌ △BCE (SAS)$；
(2) $AE = BE$。理由如下：如图，在$CE$上截取$CF = DE$，连接$BF$。在$△ADE$和$△BCF$中，$\begin{cases}AD = BC \\ ∠3 = ∠4 \\ DE = CF \end{cases}$，$∴ △ADE ≌ △BCF (SAS)$。$∴ AE = BF$，$∠AED = ∠CFB$。$∵ ∠AED + ∠BEF = 180^{\circ}$，$∠CFB + ∠EFB = 180^{\circ}$，$∴ ∠BEF = ∠EFB$。过点$B$作$BH$平分$∠FBE$交$EF$于点$H$，$∴ ∠5 = ∠6$。在$△BHF$与$△BHE$中，$\begin{cases}∠BFH = ∠BEH \\ ∠5 = ∠6 \\ BH = BH \end{cases}$，$△BHF ≌ △BHE$。$∴ BE = BF$。$∴ AE = BE$。

8. 在△ABC中,AB= AC,D、A、E三点都在直线m上,DE= 8cm.
(1)若∠BDA= ∠AEC= ∠BAC.
① 如图①,若AB⊥AC,则BD与AE的数量关系为BD = AE,CE与AD的数量关系为CE = AD；
② 如图②,猜想BD、CE与DE的数量关系并说明理由.
(2)如图③,若∠BDA= ∠AEC,BD= 6cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以x cm/s的速度由点E向点F运动,它们运动的时间为t(s). 是否存在x,使得△DAB与以A、E、C为顶点的三角形全等？若存在,求出相应的t值；若不存在,请说明理由.

答案： 解：
(1) ① $BD = AE$ $CE = AD$
② $DE = BD + CE$，理由如下：$∵ ∠BDA + ∠B + ∠BAD = 180^{\circ}$，$∠BAC + ∠CAE + ∠BAD = 180^{\circ}$，$∠BDA = ∠BAC$，$∴ ∠B = ∠CAE$。又$∵ ∠BDA = ∠AEC$，$AB = AC$，$∴ △BDA ≌ △AEC$。$∴ BD = AE$，$AD = CE$。$∴ DE = AD + AE = CE + BD$；
(2) 当$△DAB ≌ △ECA$时，$∴ AD = CE = 2t \mathrm{cm} = x \mathrm{cm}$，$BD = AE = 6 \mathrm{cm}$，$∵ DE = 8 \mathrm{cm}$，$∴ AD = DE - AE = 2 \mathrm{cm}$，$∴ 2t = x = 2$，$∴ t = 1$，$x = 2$；当$△DAB ≌ △EAC$时，$∴ AD = AE = 4 \mathrm{cm}$，$DB = EC = 6 \mathrm{cm}$，$∴ 2t = 4$，$x = 6$，$∴ t = 2$，综上所述，存在$t = 1$，$x = 2$或$t = 2$，$x = 6$使得$△ABD$与$△EAC$全等。