2024年世纪金榜高中全程学习方略高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年世纪金榜高中全程学习方略高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
2.(多选题)(2024·沈阳高一检测)已知集合A = {x|x≥ - 2},B = {x|-2≤x≤1},则下列关系正确的是 ( )
A.A = B B.A⊆B
C.B⊆A D.B⫋A
A.A = B B.A⊆B
C.B⊆A D.B⫋A
答案:
2. CD 因为集合$A = \{x|x\geq - 2\}$,$B = \{x|-2\leq x\leq1\}$,所以根据子集及真子集的定义可知$B\subseteq A$,$B\subsetneqq A$.
【典例】1.(2024·济宁高一检测)已知集合M = {1,0},则与集合M相等的集合为 ( )
A.$\{(x,y)|\begin{cases}x - y = - 1\\x + y = 1\end{cases}\}$
B.$\{(x,y)|y=\sqrt{x - 1}+\sqrt{1 - x}\}$
C.$\{x|x=\frac{(-1)^n-1}{2},n\in N\}$
D.{x|-1<x<2,x∈N}
A.$\{(x,y)|\begin{cases}x - y = - 1\\x + y = 1\end{cases}\}$
B.$\{(x,y)|y=\sqrt{x - 1}+\sqrt{1 - x}\}$
C.$\{x|x=\frac{(-1)^n-1}{2},n\in N\}$
D.{x|-1<x<2,x∈N}
答案:
【典例】1. D 对于 A 选项,$\left\{(x,y)\left|\begin{array}{l}x - y = - 1\\x + y = 1\end{array}\right.\right\}=\{(0,1)\}\neq M$,故 A 错误;
对于 B 选项,$\{(x,y)|y = \sqrt{x - 1}+\sqrt{1 - x}\}$中$\left\{\begin{array}{l}x - 1\geq0\\1 - x\geq0\end{array}\right.$,解得$x = 1$,故$\{(x,y)|y = \sqrt{x - 1}+\sqrt{1 - x}\}=\{(1,0)\}\neq M$,故 B 错误;
对于 C 选项,$\left\{x\left|x=\frac{(-1)^n - 1}{2},n\in N\right.\right\}=\{-1,0\}\neq M$,故 C 错误;
对于 D 选项,$\{x|-1\lt x\lt2,x\in N\}=\{0,1\}=M$,故 D 正确.
2. CD 因为集合$A = \{x|x\geq - 2\}$,$B = \{x|-2\leq x\leq1\}$,所以根据子集及真子集的定义可知$B\subseteq A$,$B\subsetneqq A$.
对于 B 选项,$\{(x,y)|y = \sqrt{x - 1}+\sqrt{1 - x}\}$中$\left\{\begin{array}{l}x - 1\geq0\\1 - x\geq0\end{array}\right.$,解得$x = 1$,故$\{(x,y)|y = \sqrt{x - 1}+\sqrt{1 - x}\}=\{(1,0)\}\neq M$,故 B 错误;
对于 C 选项,$\left\{x\left|x=\frac{(-1)^n - 1}{2},n\in N\right.\right\}=\{-1,0\}\neq M$,故 C 错误;
对于 D 选项,$\{x|-1\lt x\lt2,x\in N\}=\{0,1\}=M$,故 D 正确.
2. CD 因为集合$A = \{x|x\geq - 2\}$,$B = \{x|-2\leq x\leq1\}$,所以根据子集及真子集的定义可知$B\subseteq A$,$B\subsetneqq A$.
3.(教材提升例3)判断下列各组中集合之间的关系:
①A = {x|x是12的约数},B = {x|x是36的约数};
②A = {x|x² - x = 0},B = {x∈R|x² + 1 = 0};
③A = {x|x是平行四边形},B = {x|x是菱形},C = {x|x是四边形},D = {x|x是正方形};
④$M=\{x|x=\frac{n}{2},n\in Z\}$,$N=\{x|x=\frac{1}{2}+n,n\in Z\}$.
①A = {x|x是12的约数},B = {x|x是36的约数};
②A = {x|x² - x = 0},B = {x∈R|x² + 1 = 0};
③A = {x|x是平行四边形},B = {x|x是菱形},C = {x|x是四边形},D = {x|x是正方形};
④$M=\{x|x=\frac{n}{2},n\in Z\}$,$N=\{x|x=\frac{1}{2}+n,n\in Z\}$.
答案:
3.【解析】①因为若 x 是 12 的约数,则必定是 36 的约数,反之不成立,所以.
②因为,,所以.
③由图形的特点可画出维恩图如图所示,
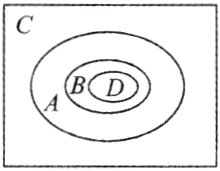
从而.
④方法一:对于集合 M,其组成元素是,分子部分表示所有的整数;对于集合 N,其组成元素是,分子部分表示所有的奇数. 由真子集的概念知,.
方法二:用列举法表示集合如下:
,
,所以.
3.【解析】①因为若 x 是 12 的约数,则必定是 36 的约数,反之不成立,所以.
②因为,,所以.
③由图形的特点可画出维恩图如图所示,

从而.
④方法一:对于集合 M,其组成元素是,分子部分表示所有的整数;对于集合 N,其组成元素是,分子部分表示所有的奇数. 由真子集的概念知,.
方法二:用列举法表示集合如下:
,
,所以.
指出下列各对集合之间的关系.
(1)A = {-1,1},B = {(-1,-1),(-1,1),(1,-1),(1,1)};
(2)A = {x|-1<x<4},B = {x|x - 5<0};
(3)A = {x|x是等边三角形},B = {x|x是等腰三角形};
(4)$M=\{x|x = 2n - 1,n\in N^*\}$,$N=\{x|x = 2n+1,n\in N^*\}$;
(5)A = {x|x = 2a + 3b,a∈Z,b∈Z},B = {x|x = 4m - 3n,m∈Z,n∈Z}.
(1)A = {-1,1},B = {(-1,-1),(-1,1),(1,-1),(1,1)};
(2)A = {x|-1<x<4},B = {x|x - 5<0};
(3)A = {x|x是等边三角形},B = {x|x是等腰三角形};
(4)$M=\{x|x = 2n - 1,n\in N^*\}$,$N=\{x|x = 2n+1,n\in N^*\}$;
(5)A = {x|x = 2a + 3b,a∈Z,b∈Z},B = {x|x = 4m - 3n,m∈Z,n∈Z}.
答案:
【解析】
(1)集合 A 的代表元素是数,集合 B 的代表元素是有序实数对,故 A 与 B 之间无包含关系.
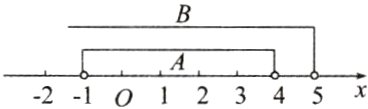
(2)集合$B = \{x|x\lt5\}$,用数轴表示集合 A,B 如图所示,
由图可知$A\subsetneqq B$.
(3)等边三角形是三边相等的三角形,等腰三角形是两边相等的三角形,故$A\subsetneqq B$.
(4)两个集合都表示正奇数组成的集合,但由于$n\in N^{*}$,因此集合 M 含有元素“1”,而集合 N 不含元素“1”,故$N\subsetneqq M$.
(5)$A = \{x|x = 2a + 3b,a\in Z,b\in Z\}$,因为任意$k\in Z$,$k = 2\times(-k)+3k\in A$,所以$A = \{x|x = 2a + 3b,a\in Z,b\in Z\}=Z$,
因为任意$k\in Z$,$k = 4k - 3k\in B$,所以$B = \{x|x = 4m - 3n,m\in Z,n\in Z\}=Z$,所以$A = B = Z$.
【解析】
(1)集合 A 的代表元素是数,集合 B 的代表元素是有序实数对,故 A 与 B 之间无包含关系.
(2)集合$B = \{x|x\lt5\}$,用数轴表示集合 A,B 如图所示,
由图可知$A\subsetneqq B$.

(3)等边三角形是三边相等的三角形,等腰三角形是两边相等的三角形,故$A\subsetneqq B$.
(4)两个集合都表示正奇数组成的集合,但由于$n\in N^{*}$,因此集合 M 含有元素“1”,而集合 N 不含元素“1”,故$N\subsetneqq M$.
(5)$A = \{x|x = 2a + 3b,a\in Z,b\in Z\}$,因为任意$k\in Z$,$k = 2\times(-k)+3k\in A$,所以$A = \{x|x = 2a + 3b,a\in Z,b\in Z\}=Z$,
因为任意$k\in Z$,$k = 4k - 3k\in B$,所以$B = \{x|x = 4m - 3n,m\in Z,n\in Z\}=Z$,所以$A = B = Z$.
查看更多完整答案,请扫码查看


