《2024年世纪金榜高中全程学习方略高中数学必修第一册人教版》

一、命题的否定
1.命题的否定：
一般地，对命题p加以______，就得到一个新的命题，记作_____，读作“非p”或“p的否定”.
2.命题¬p的真假性：
命题¬p的真假性可以用下表(真值表)表示：

显然，¬p与p不能同真或同假，其中一个为真，另一个必定为假，它们是互为否定的，从而有¬(¬p)=p.

答案： 1.否定  “¬p”

教材挖掘(P30练习AT1)
(1)如果p是真命题，那么¬p是真命题还是假命题？
(2)如果¬q是真命题，那么q是真命题还是假命题？

答案： 提示：
(1)¬p 是假命题；
(2)q 是假命题.

二、含量词的命题的否定

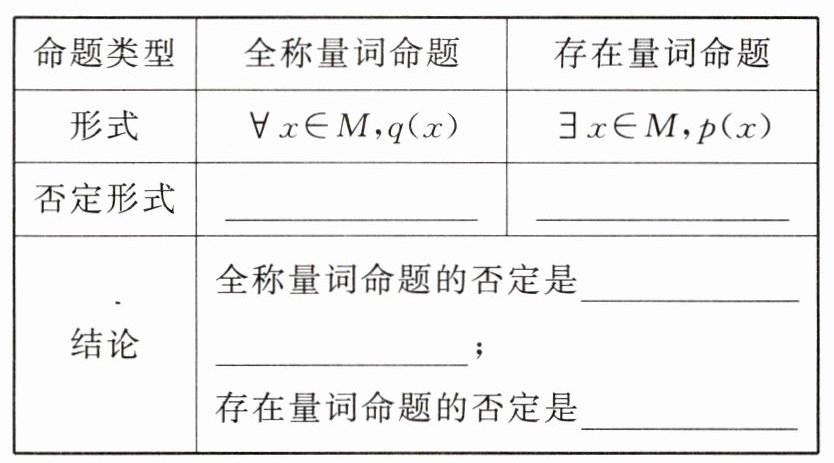
答案： ∃x∈M,¬q(x) ∀x∈M,¬p(x) 存在量词命题 全称量词命题

如何写出下列存在量词命题的否定？
(1)存在凸n边形(n∈N，且n≥3)，它的内角和等于720°；
(2)∃x∈N，x²的个位数字等于3.

答案： 提示：
(1)任意凸 n 边形(n∈N，且 n≥3)，它的内角和不等于 720°；
(2)∀x∈N,x² 的个位数字不等于 3.

(1)命题¬p的否定是p. （ ）
(2)∃x∈M，p(x)与∀x∈M，¬p(x)的真假性相反. （ ）
(3)从存在量词命题的否定看，是对“量词”和“p(x)”同时否定. （ ）
(4)全称量词命题是陈述某集合中所有元素都具有某种性质的命题. （ ）

答案：
(1)√ 提示：命题 p 与¬p 互为否定.
(2)√ 提示：∃x∈M,p(x)与∀x∈M,¬p(x)互为否定，其真假性为一真一假.
(3)× 提示：存在量词命题的否定是全称量词命题，只是对“p(x)”进行否定，而将“存在量词”调整为“全称量词”，不能将其理解为“同时否定”.
(4)√ 提示：根据全称量词命题的定义可知正确.