《2024年世纪金榜高中全程学习方略高中数学必修第一册人教版》

【典例】(2024·锦州高一检测)已知集合A = {x|a - 1＜x＜2a + 3，a＞0}，B = {x|-2＜x＜4}.
(1)当a = 2时，求A∪B；
(2)若A∩B = ∅，求实数a的取值范围.

答案： [解析]
(1)因为$a = 2$，所以$A = \{x|1\lt x\lt7\}$，而$B = \{x|-2\lt x\lt4\}$，所以$A\cup B = \{x|-2\lt x\lt7\}$；
(2)因为$A\cap B = \varnothing$，
　①若$A = \varnothing$时，$a - 1\geq2a + 3$，得$a\leq - 4$，而$a\gt0$，所以不存在这种情况；
　②若$A\neq\varnothing$时，$a - 1\geq4$，或$2a + 3\leq - 2$，
　由$a - 1\geq4\Rightarrow a\geq5$，显然满足$a\gt0$；
　由$2a + 3\leq - 2\Rightarrow a\leq - \frac{5}{2}$，而$a\gt0$，所以不存在这种情况，
　综上所述，实数$a$的取值范围是$[5,+\infty)$。

已知集合A = {x|-3＜x≤4}，集合B = {x|k + 1≤x≤2k - 1}，且A∪B = A，试求k的取值范围.

答案：
[解析]因为$A\cup B = A$，所以$B\subseteq A$，所以分$B = \varnothing$和$B\neq\varnothing$两种情况讨论。
　①当$B = \varnothing$时，$k + 1\gt2k - 1$，解得$k\lt2$。
　②当$B\neq\varnothing$时，如图所示:
　　　　　　　　　
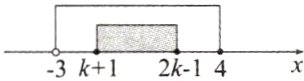
　　　　　　　根据数轴可得$\begin{cases}k + 1\leq2k - 1\\-3\lt k + 1\\2k - 1\leq4\end{cases}$，解得$2\leq k\leq\frac{5}{2}$。
　综合①②可得，$k$的取值范围是$\{k|k\leq\frac{5}{2}\}$。