《2025年名校课堂九年级数学全一册北师大版四川专版》

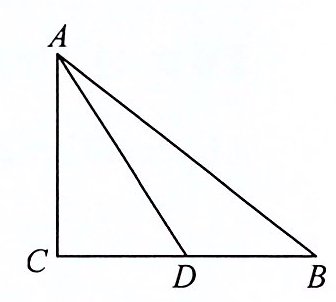
【例】如图，在 $ Rt \triangle ABC $ 中，$ \angle C = 90^{\circ} $，$ D $ 为 $ BC $ 的中点，$ AC = 3 $，$ \tan \angle CDA = \frac{3}{2} $，求 $ \sin \angle DBA $ 的值.
【分析】在 $ Rt \triangle ABC $ 中，$ \sin \angle DBA = \frac{AC}{AB} $，而 $ AC $ 已知，故求出 $ AB $ 即可. 在 $ Rt \triangle ACD $ 中，根据 $ \tan \angle CDA = \frac{AC}{CD} = \frac{3}{2} $，$ AC = 3 $，可求出 $ CD $，进而根据勾股定理可求出 $ AB $.
【解答】

【方法指导】解直角三角形选择三角函数关系式时，应遵循“有弦用弦，无弦用切，宁乘勿除，取原（原始数据）避中（中间求出的数据）”的原则.

答案： 【例】解:在Rt△ACD中,tan∠CDA=$\frac{3}{2}$,AC=3,
∴$\frac{AC}{CD}$=$\frac{3}{2}$=$\frac{3}{CD}$,
∴CD=2.
∵D为BC的中点,
∴BC=2CD=4.在Rt△ABC中,AB=$\sqrt{AC^2+BC^2}$=$\sqrt{3^2+4^2}$=5.
∴sin∠DBA=$\frac{AC}{AB}$=$\frac{3}{5}$.

【变式】如图，$ \triangle ABC $ 中，$ \angle A = 30^{\circ} $，$ AC = 2\sqrt{3} $，$ \tan B = \frac{\sqrt{3}}{2} $，则 $ AB = $5.

答案： 【变式】5

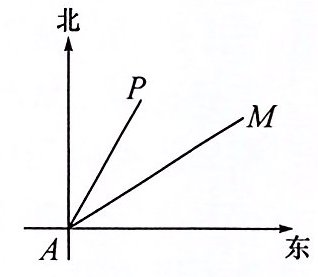
【例】如图所示，小岛 $ P $ 的周围 $ 20\sqrt{2} $ 海里内有暗礁，某渔船沿北偏东 $ 60^{\circ} $ 的 $ AM $ 方向航行，在 $ A $ 处测得小岛 $ P $ 的方向为北偏东 $ 30^{\circ} $，且距点 $ A $ 处 $ 40 $ 海里，该渔船若不改变航向，有无触礁的可能？若有可能触礁，则该渔船在 $ A $ 处至少应再向北偏东偏离多大角度才能脱险？
【分析】先将航海问题抽象成纯数学问题，建立起“解直角三角形”的数学模型，有无触礁可能，即是点 $ P $ 到 $ AM $ 的距离是否大于 $ 20\sqrt{2} $ 海里的问题。过点 $ P $ 作 $ PC \perp AM $ 于点 $ C $，在 $ \triangle PAC $ 中，求出 $ PC $，与 $ 20\sqrt{2} $ 作比较。若 $ PC ＜ 20\sqrt{2} $，则有触礁的可能，就必须改变航线。
【解答】

答案： 解:过点 P 作 PC⊥AM 于点 C. 在 Rt△PAC 中,PA=40 海里,∠PAC=30°,
∴PC=PA·sin∠PAC=PA·sin30°=40×$\frac{1}{2}$=20(海里).
∵20＜20$\sqrt{2}$,该渔船有触礁危险,要改变航向.设渔船按 AN 方向航行刚好可以脱险,过点 P 作 PD⊥AN 于点 D,PD=20$\sqrt{2}$海里.在 Rt△PAD 中,sin∠PAD=$\frac{PD}{PA}$=$\frac{20\sqrt{2}}{40}$=$\frac{\sqrt{2}}{2}$,
∴∠PAD=45°,
∴∠MAN=∠PAD-∠PAC=45°-30°=15°.
∴渔船在 A 处至少应再向北偏东偏离15°,才能脱险.