2025年名校课堂九年级数学全一册北师大版四川专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校课堂九年级数学全一册北师大版四川专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
【例】 家住某一小区一单元的甲、乙二人同时从地下车库进入电梯回家,已知两人到 1 至 4 层的任意一层出电梯,并设甲在 $a$ 层出电梯,乙在 $b$ 层出电梯。
(1)用画树状图法或列表法表示 $(a,b)$ 的所有可能结果,并求甲、乙二人在同一层楼出电梯的概率。
(2)小亮和小芳打赌,若甲、乙住在同楼层或相邻楼层,则小亮胜,否则小芳胜。判断上述游戏是否公平,请说明理由。
【解答】
(1)用画树状图法或列表法表示 $(a,b)$ 的所有可能结果,并求甲、乙二人在同一层楼出电梯的概率。
(2)小亮和小芳打赌,若甲、乙住在同楼层或相邻楼层,则小亮胜,否则小芳胜。判断上述游戏是否公平,请说明理由。
【解答】
答案:
解:
(1)列表略.一共出现 16 种结果,每种结果都为等可能事件,其中甲、乙二人在同一层楼出电梯的有 4 种结果,所以 $ P(甲、乙二人在同一层楼出电梯)=\frac{4}{16}=\frac{1}{4} $.
(2)不公平.理由如下:由
(1)表知,甲、乙住在同楼层或相邻楼层有 10 种结果,故 $ P(小亮胜)=\frac{10}{16}=\frac{5}{8} $,$ P(小芳胜)=1-\frac{5}{8}=\frac{3}{8} $.因为 $ \frac{5}{8}>\frac{3}{8} $,所以上述游戏不公平.
(1)列表略.一共出现 16 种结果,每种结果都为等可能事件,其中甲、乙二人在同一层楼出电梯的有 4 种结果,所以 $ P(甲、乙二人在同一层楼出电梯)=\frac{4}{16}=\frac{1}{4} $.
(2)不公平.理由如下:由
(1)表知,甲、乙住在同楼层或相邻楼层有 10 种结果,故 $ P(小亮胜)=\frac{10}{16}=\frac{5}{8} $,$ P(小芳胜)=1-\frac{5}{8}=\frac{3}{8} $.因为 $ \frac{5}{8}>\frac{3}{8} $,所以上述游戏不公平.
【变式】 两个可以自由转动的转盘 $A$,$B$,其中转盘 $A$ 被 6 等分,且标上数字 1,2,3,4,5,6,转盘 $B$ 被 4 等分,分别标上数字 7,8,9,10,转动两个转盘,当转盘停止时,若两个数字指针所指向数字之和为奇数,则甲胜;若两个数字之和为偶数,则乙胜。此游戏对甲、乙二人
公平
(填“公平”或“不公平”)。
答案:
公平
【例】 用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则可配成紫色的概率是

【分析】 如图 1,将第二个转盘中的蓝色部分等分成两部分,分别记为蓝 1、蓝 2. 画树状图如图 2:
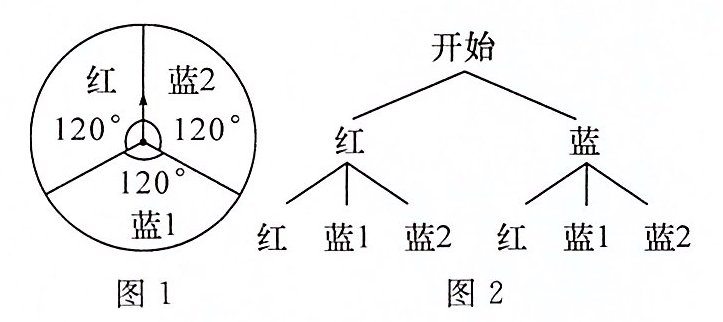
∵共有 6 种等可能的结果,其中可配成紫色的有 3 种:(红,蓝 1),(红,蓝 2),(蓝,红),∴$ P $(可配成紫色)$ = \dfrac{1}{2} $。
【方法指导】 当试验对象重复(出现多个)时,取出其中一个属性相同的试验对象的概率是不相等的,这时需要加顺序数字予以区别,然后再画树状图或列表格表示试验可能出现的各种结果. 不过仍需注意“放回”与“不放回”的区别。
$\frac{1}{2}$
。
【分析】 如图 1,将第二个转盘中的蓝色部分等分成两部分,分别记为蓝 1、蓝 2. 画树状图如图 2:

∵共有 6 种等可能的结果,其中可配成紫色的有 3 种:(红,蓝 1),(红,蓝 2),(蓝,红),∴$ P $(可配成紫色)$ = \dfrac{1}{2} $。
【方法指导】 当试验对象重复(出现多个)时,取出其中一个属性相同的试验对象的概率是不相等的,这时需要加顺序数字予以区别,然后再画树状图或列表格表示试验可能出现的各种结果. 不过仍需注意“放回”与“不放回”的区别。
答案:
$\frac{1}{2}$
查看更多完整答案,请扫码查看


