《2025年名校课堂九年级数学全一册北师大版四川专版》

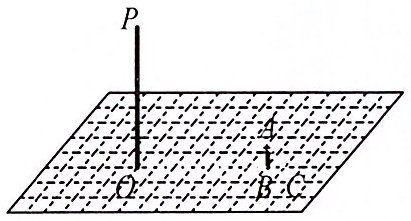
【例】如图，小亮晚上在广场上乘凉. 图中线段 $ AB $ 表示站在广场上的小亮，线段 $ PO $ 表示直立在广场上的灯杆，点 $ P $ 表示照明灯.
（1）请在图中画出小亮在照明灯（$ P $）照射下的影子.
（2）如果灯杆 $ PO = 12 \, m $，小亮的身高 $ AB = 1.6 \, m $，小亮与灯杆的距离 $ BO = 13 \, m $，请求出小亮影子的长.
【分析】（1）直接连接点光源和小亮头顶端形成的直线与 $ OB $ 延长线的交点即是影子的顶端.
（2）根据中心投影的特点可知 $ \triangle CAB \sim \triangle CPO $，利用相似比即可求解.
【解答】

【方法指导】解题的关键是由中心投影的特点可知存在着三角形相似，利用其相似比构造等量关系求出所需要的线段.

答案： 解:
(1)连接 PA 并延长交 OB 的延长线于点 C,线段 BC 就是小亮在照明灯(P)照射下的影子.
(2)
∵∠C=∠C,∠ABC=∠POC=90°,
∴△CAB∽△CPO.
∴$\frac{AB}{PO}=\frac{CB}{CO}$,即$\frac{1.6}{12}=\frac{CB}{13+BC}$.
∴BC=2.
∴小亮影子的长度为2 m.

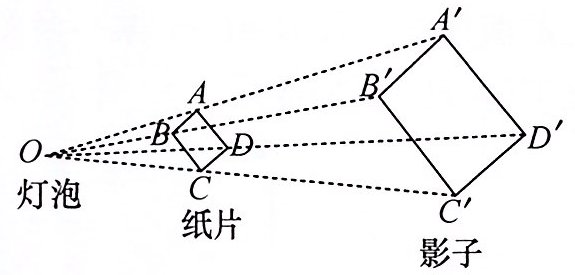
【变式】如图，小莉用灯泡 $ O $ 照射一个矩形硬纸片 $ ABCD $，在墙上形成矩形影子 $ A'B'C'D' $，现测得 $ OA = 2 \, cm $，$ OA' = 5 \, cm $，纸片 $ ABCD $ 的面积为 $ 8 \, cm^2 $，则影子 $ A'B'C'D' $ 的面积为50 $ cm^2 $.

答案： 50