《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 下列二次根式中，能与$\sqrt{2}$合并的是 （ ）
A. $\sqrt{24}$
B. $\sqrt{32}$
C. $\sqrt{96}$
D. $\sqrt{\frac{3}{4}}$

答案： B 解析：$\sqrt{32}=\sqrt{16×2}=4\sqrt{2}$，能与$\sqrt{2}$合并。 名师点睛：二次根式能合并指的就是二次根式化为最简二次根式后被开方数相同，这样的二次根式才能合并。

2 (原创题)下列各组二次根式中，能合并的一组是 （ ）
A. $\sqrt{3}$，$\sqrt{6}$
B. $\sqrt{12}$，$\sqrt{24}$
C. $\sqrt{\frac{2}{3}}$，$\sqrt{\frac{3}{2}}$
D. $\sqrt{\frac{1}{2}}$，$\sqrt{\frac{1}{3}}$

答案： C 解析：$\sqrt{\frac{2}{3}}=\sqrt{\frac{6}{9}}=\frac{1}{3}\sqrt{6}$，$\sqrt{\frac{3}{2}}=\sqrt{\frac{6}{4}}=\frac{1}{2}\sqrt{6}$。故选C。

3 计算$\sqrt{12}+\sqrt{27}$的结果是 （ ）
A. $3\sqrt{3}$
B. $5\sqrt{3}$
C. $\sqrt{39}$
D. $13\sqrt{3}$

答案： B 解析：$\sqrt{12}+\sqrt{27}=2\sqrt{3}+3\sqrt{3}=5\sqrt{3}$。

4 下列运算中，结果不正确的是 （ ）
A. $\sqrt{2}\times\sqrt{3}=\sqrt{6}$
B. $\sqrt{15}\div\sqrt{5}=\sqrt{3}$
C. $\sqrt{8}-\sqrt{2}=\sqrt{2}$
D. $\sqrt{2}+\sqrt{3}=\sqrt{5}$

答案： D

5 计算$\sqrt{20a}-\sqrt{45a}$的结果为 （ ）
A. $\sqrt{5a}$
B. $-\sqrt{5a}$
C. $-\sqrt{5}a$
D. $5\sqrt{5a}$

答案： B 解析：$\sqrt{20a}-\sqrt{45a}=2\sqrt{5a}-3\sqrt{5a}=-\sqrt{5a}$。

6 (2022·哈尔滨)计算$\sqrt{3}+3\sqrt{\frac{1}{3}}$的结果是_______.

答案： $2\sqrt{3}$ 解析：原式$=\sqrt{3}+3×\frac{\sqrt{3}}{3}=\sqrt{3}+\sqrt{3}=2\sqrt{3}$。故答案为$2\sqrt{3}$。

7 已知三个正方形的面积分别为12 $cm^{2}$、27 $cm^{2}$、48 $cm^{2}$，则它们的周长和等于_______$cm$.

答案： $36\sqrt{3}$ 解析：它们的周长和为$4\sqrt{12}+4\sqrt{27}+4\sqrt{48}=4(2\sqrt{3}+3\sqrt{3}+4\sqrt{3})=4×9\sqrt{3}=36\sqrt{3}(cm)$。

8 计算：$\sqrt{2}\div\sqrt{6}+\sqrt{15}\div\sqrt{5}=$_______.

答案： $\frac{4}{3}\sqrt{3}$ 解析：原式$=\sqrt{\frac{1}{3}}+\sqrt{3}=\frac{\sqrt{3}}{3}+\sqrt{3}=\frac{4}{3}\sqrt{3}$。

9 (原创题)有下列等式：①$\sqrt{a + b}=\sqrt{a}\cdot\sqrt{b}$；②$\sqrt{a}+\sqrt{b}=\sqrt{ab}$；③$\sqrt{a}+\sqrt{b}=\sqrt{a + b}$；④$\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}$.其中正确的个数为 （ ）
A. 0
B. 1
C. 2
D. 3

答案： B 解析：只有$\sqrt{a}·\sqrt{b}=\sqrt{ab}$正确。

10 已知$\sqrt{24m}+4\sqrt{\frac{3m}{2}}+m\sqrt{\frac{6}{m}} = 30$，则$m$的值为 （ ）
A. 3
B. 5
C. 6
D. 8

答案： C 解析：$\because\sqrt{24m}+4\sqrt{\frac{3m}{2}}+m\sqrt{\frac{6}{m}}=30$，$\therefore\sqrt{24m}+\sqrt{24m}+\sqrt{6m}=30$，$\therefore5\sqrt{6m}=30$，$\therefore\sqrt{6m}=6$，$\therefore m = 6$。故选C。

11 已知$m=\frac{-b+\sqrt{b^{2}-4ac}}{2a}$，$n=\frac{-b-\sqrt{b^{2}-4ac}}{2a}$，则$m + n=$ （ ）
A. $\frac{\sqrt{b^{2}-4ac}}{a}$
B. $-\frac{b}{a}$
C. $-\frac{\sqrt{b^{2}-4ac}}{a}$
D. $\frac{b}{a}$

答案： B 解析：$m + n=\frac{-b+\sqrt{b^{2}-4ac}}{2a}+\frac{-b-\sqrt{b^{2}-4ac}}{2a}=\frac{-b+\sqrt{b^{2}-4ac}-b-\sqrt{b^{2}-4ac}}{2a}=\frac{-2b}{2a}=-\frac{b}{a}$。

12 如图，点$A$在数轴上表示的数是$\sqrt{3}-\sqrt{2}$，点$B$在数轴上表示的数是$\sqrt{2}-\sqrt{3}$，点$C$与点$B$关于点$A$对称，则点$C$表示的数是（ ）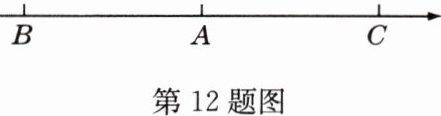
A. $2\sqrt{3}-2\sqrt{2}$
B. $3\sqrt{2}-2\sqrt{3}$
C. $3\sqrt{3}-3\sqrt{2}$
D. $3\sqrt{2}-3\sqrt{3}$

答案： C 解析：设C表示的数是$x$，则$x - (\sqrt{3}-\sqrt{2})=\sqrt{3}-\sqrt{2}-(\sqrt{2}-\sqrt{3})$，得$x = 3\sqrt{3}-3\sqrt{2}$。

13 (原创题)下列计算中，正确的是 （ ）
A. $\sqrt{a}+\sqrt{2a}=\sqrt{3a}$
B. $\sqrt{3}a-\sqrt{2}a=a$
C. $\sqrt{3}a-\sqrt{3}b=\sqrt{3}(a - b)$
D. $3\sqrt{2a}+2\sqrt{3a}=5\sqrt{5a}$

答案： C