《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1（2022·营口，中）如图，在矩形ABCD中，点M在AB边上，把△BCM沿直线CM折叠，使点B落在AD边上的点E处，过点B作BF⊥EC，垂足为F，若CD = 1，CF = 2，则线段AE的长为（ ）


A. $\sqrt{5}-2$
B. $\sqrt{3}-1$
C. $\frac{1}{3}$
D. $\frac{1}{2}$

答案： **A**\n解析：因为四边形$ABCD$是矩形，所以$BC = AD$，$\angle ABC=\angle D = 90^{\circ}$，$AD// BC$，则$\angle DEC=\angle FCB$。\n又因为$BF\perp EC$，所以$\angle BFC=\angle CDE$。\n由于把$\triangle BCM$沿直线$CM$折叠，使点$B$落在$AD$边上的点$E$处，所以$BC = EC$。\n在$\triangle BFC$与$\triangle CDE$中，$\begin{cases}\angle FCB=\angle DEC\\\angle BFC=\angle CDE\\BC = EC\end{cases}$，所以$\triangle BFC\cong\triangle CDE(AAS)$，则$DE = CF = 2$。\n进而$CE=\sqrt{CD^{2}+DE^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$AD = BC = CE=\sqrt{5}$，$AE=AD - DE=\sqrt{5}-2$。故选$A$。

2（2022·重庆A卷，中）如图，在正方形ABCD中，AE平分∠BAC交BC于点E，点F是边AB上一点，连接DF，若BE = AF，则∠CDF的度数为（ ）

A. 45°
B. 60°
C. 67.5°
D. 77.5°

答案： **C**\n解析：因为四边形$ABCD$是正方形，所以$AD = AB$，$\angle DAF=\angle B=\angle ADC = 90^{\circ}$，$\angle BAC = 45^{\circ}$。\n因为$AE$平分$\angle BAC$交$BC$于点$E$，所以$\angle BAE=\frac{1}{2}\angle BAC = 22.5^{\circ}$。\n在$\triangle ABE$和$\triangle DAF$中，$\begin{cases}AB = DA\\\angle B=\angle DAF\\BE = AF\end{cases}$，所以$\triangle ABE\cong\triangle DAF(SAS)$，则$\angle ADF=\angle BAE = 22.5^{\circ}$。\n所以$\angle CDF=\angle ADC-\angle ADF=90^{\circ}-22.5^{\circ}=67.5^{\circ}$。故选$C$。

3（2022·无锡，中）下列命题中，是真命题的有（ ）
①对角线相等且互相平分的四边形是矩形；
②对角线互相垂直的四边形是菱形；
③四边相等的四边形是正方形；
④四边相等的四边形是菱形.
A. ①②
B. ①④
C. ②③
D. ③④

答案： **B**

4（2022·无锡，中）如图，在□ABCD中，AD = BD，∠ADC = 105°，点E在AD上，∠EBA = 60°，则$\frac{ED}{CD}$的值是（ ）


A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{2}}{2}$

答案： **D**\n解析：如图，过点$B$作$BF\perp AD$于点$F$。\n因为四边形$ABCD$是平行四边形，所以$CD = AB$，$CD// AB$，$\angle ADC+\angle BAD = 180^{\circ}$。\n又因为$\angle ADC = 105^{\circ}$，所以$\angle A = 75^{\circ}$。\n因为$\angle ABE = 60^{\circ}$，所以$\angle AEB=180^{\circ}-\angle A-\angle ABE = 45^{\circ}$。\n因为$BF\perp AD$，所以$\angle BFD = 90^{\circ}$，$\angle EBF=\angle AEB = 45^{\circ}$，则$BF = FE$。\n因为$AD = BD$，所以$\angle ABD=\angle A = 75^{\circ}$，$\angle ADB = 30^{\circ}$。\n设$BF = EF = x$，则$BD = 2x$，由勾股定理，得$DF=\sqrt{3}x$。\n所以$DE=DF - EF=(\sqrt{3}-1)x$，$AF=AD - DF=BD - DF=(2 - \sqrt{3})x$。\n由勾股定理，得$AB^{2}=AF^{2}+BF^{2}=(2 - \sqrt{3})^{2}x^{2}+x^{2}=(8 - 4\sqrt{3})x^{2}$。\n所以$\frac{DE^{2}}{AB^{2}}=\frac{(\sqrt{3}-1)^{2}x^{2}}{(8 - 4\sqrt{3})x^{2}}=\frac{1}{2}$，$\frac{DE}{AB}=\frac{\sqrt{2}}{2}$。\n因为$AB = CD$，所以$\frac{DE}{CD}=\frac{\sqrt{2}}{2}$。故选$D$。

5（2022·绍兴，难）如图，在平行四边形ABCD中，AD = 2AB = 2，∠ABC = 60°，E，F是对角线BD上的动点，且BE = DF，M，N分别是边AD，边BC上的动点.有下列四种说法：①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在无数个正方形MENF.其中正确的个数是（ ）

A. 1
B. 2
C. 3
D. 4

答案： **C**\n解析：如图，连接$AC$交$BD$于点$O$，连接$ME$，$MF$，$NF$，$EN$，$MN$。\n因为四边形$ABCD$是平行四边形，所以$OA = OC$，$OB = OD$。\n因为$BE = DF$，所以$OE = OF$。\n若$M$，$N$过点$O$，则四边形$MENF$就是平行四边形，所以存在无数个平行四边形$MENF$，故①正确；\n若$MN = EF$，且$MN$过点$O$，则四边形$MENF$是矩形，因为点$E$，$F$是$BD$上的动点，所以存在无数个矩形$MENF$，故②正确；\n若$MN\perp EF$，且$MN$过点$O$，则四边形$MENF$是菱形，因为点$E$，$F$是$BD$上的动点，所以存在无数个菱形$MENF$，故③正确；\n若$MN = EF$，$MN\perp EF$，且$MN$过点$O$，则四边形$MENF$是正方形，而符合要求的正方形只有一个，故④错误。故选$C$。

6（2022·台州，中）如图，△ABC的边BC长为4 cm.将△ABC平移2 cm得到△A'B'C'，且BB'⊥BC，则阴影部分的面积为________ $cm^{2}$.

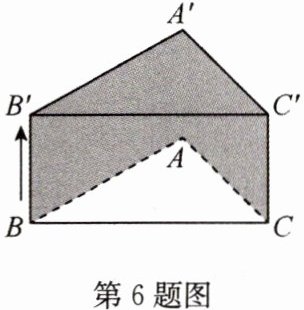
答案： **8**

7（2022·盘锦，中）如图，四边形ABCD为矩形，AB = $\sqrt{2}$，AD = 3，点E为边BC上一点，将△DCE沿DE翻折，点C的对应点为点F，过点F作DE的平行线交AD于点G，交BC于点H.若点G是边AD的三等分点，则FG的长是________.

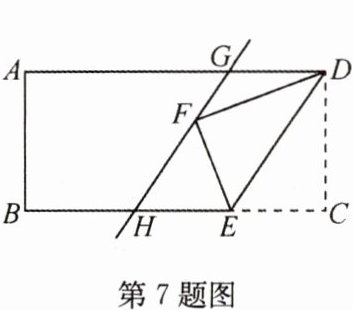
答案： $\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$\n解析：如图①，过点$E$作$EM\perp GH$于点$M$。\n因为$DE// GH$，$AD// BC$，所以四边形$HEDG$是平行四边形，$HE = GD=\frac{1}{3}AD = 1$。\n因为将$\triangle CDE$沿$DE$翻叠，所以$\angle FED=\angle CED$。\n因为$\angle MED = 90^{\circ}$，即$\angle FEM+\angle FED = 90^{\circ}$，$\angle CED+\angle HEM = 90^{\circ}$，所以$\angle HEM=\angle FEM$。\n又因为$\angle EMF=\angle EMH = 90^{\circ}$，$ME = ME$，所以$\triangle HEM\cong\triangle FEM$，$HM = MF$，$EF = HE = 1$，$EF = EC = 1$。\n因为四边形$ABCD$是矩形，所以$\angle C = 90^{\circ}$，$DC = AB=\sqrt{2}$。\n在$Rt\triangle EDC$中，$DE=\sqrt{DC^{2}+EC^{2}}=\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{3}$，$GH = DE=\sqrt{3}$。\n因为$ME\perp HG$，$HG// DE$，所以$S_{\triangle DEF}=\frac{1}{2}ME\times DE=S_{\triangle DEC}=\frac{1}{2}DC\times EC$，$ME=\frac{DC\times EC}{DE}=\frac{\sqrt{2}\times1}{\sqrt{3}}=\frac{\sqrt{6}}{3}$。\n在$Rt\triangle HME$中，$HM=\sqrt{HE^{2}-ME^{2}}=\sqrt{1 - (\frac{\sqrt{6}}{3})^{2}}=\frac{\sqrt{3}}{3}$，$FG=HG - HF=HG - 2HM=\sqrt{3}-\frac{2\sqrt{3}}{3}=\frac{\sqrt{3}}{3}$。\n如图②，当$AG=\frac{1}{3}AD = 1$时，同理可得$HE = GD=AD - AG=3 - 1 = 2$，$EC = EF = HE = 2$。\n$DE=\sqrt{2^{2}+(\sqrt{2})^{2}}=\sqrt{6}$，$ME=\frac{DC\times EC}{DE}=\frac{\sqrt{2}\times2}{\sqrt{6}}=\frac{2\sqrt{3}}{3}$。\n在$Rt\triangle HME$中，$HM=\sqrt{HE^{2}-ME^{2}}=\sqrt{2^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$，$FG=HF - HG=2HM - HG=\frac{4\sqrt{6}}{3}-\sqrt{6}=\frac{\sqrt{6}}{3}$。故答案为$\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$。

8（2022·龙东，中）如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD = 60°，AD =
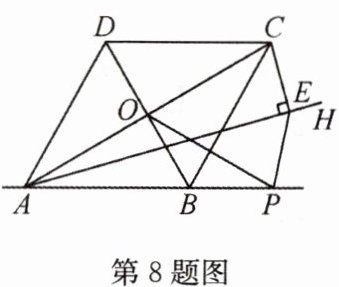
3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP + PE的最小值是________.

答案： $\frac{3\sqrt{6}}{2}$\n解析：如图，作点$O$关于直线$AB$的对称点$F$，连接$OF$交$AB$于点$G$，连接$FE$交直线$AB$于点$P'$，连接$P'O$，$OE$，则$P'O = PF$，此时，$P'O+P'E$最小，最小值$ = EF$。\n因为四边形$ABCD$是菱形，所以$AC\perp BD$，$OA = OC$，$OB = OD$，$AD = AB = 3$。\n因为$\angle BAD = 60^{\circ}$，所以$\triangle ABD$是等边三角形，$BD = AB = 3$，$\angle BAO = 30^{\circ}$，$OB=\frac{3}{2}$，$OA=\frac{3\sqrt{3}}{2}$。\n因为点$O$关于直线$AB$的对称点为点$F$，所以$OF\perp AB$，$OF = 2OG=OA=\frac{3\sqrt{3}}{2}$，$\angle AOG = 60^{\circ}$。\n因为$CE\perp AH$于点$E$，$OA = OC$，所以$OE = OC=OA=\frac{3\sqrt{3}}{2}$。\n因为$AH$平分$\angle BAC$，所以$\angle CAE = 15^{\circ}$，$\angle AEO=\angle CAE = 15^{\circ}$，$\angle COE=\angle AEO+\angle CAE = 30^{\circ}$，$\angle COE+\angle AOG = 30^{\circ}+60^{\circ}=90^{\circ}$，$\angle FOE = 90^{\circ}$。\n由勾股定理，得$EF=\sqrt{OF^{2}+OE^{2}}=\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}=\frac{3\sqrt{6}}{2}$，$PO + PE$的最小值是$\frac{3\sqrt{6}}{2}$。故答案为$\frac{3\sqrt{6}}{2}$。