第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
1 下列命题正确的是 ( )
A. 对角线相等的四边形是菱形
B. 对角线互相垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形
D. 对角线互相垂直的平行四边形是菱形
A. 对角线相等的四边形是菱形
B. 对角线互相垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形
D. 对角线互相垂直的平行四边形是菱形
答案:
D
2 已知□ABCD的对角线相交于点O,有下列条件:①AC⊥BD;②AB = BC;③AC平分∠BAD. 其中使得□ABCD是菱形的条件有 ( )
A. 0个
B. 1个
C. 2个
D. 3个
A. 0个
B. 1个
C. 2个
D. 3个
答案:
D
3(2022·营口)如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是________.(写出一个即可)
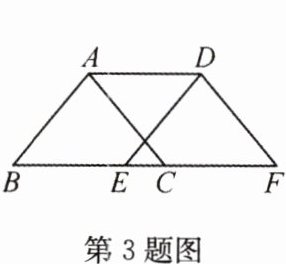

答案:
AB = BE(答案不唯一)
4 如图,在△ABC中,D是BC的中点,点E,F分别在线段AD及其延长线上,且DE = DF. 给出下列条件:①BE⊥EC;②BF//CE;③AB = AC. 从中选择一个条件使四边形BECF是菱形,你认为这个条件是________.(填写序号)
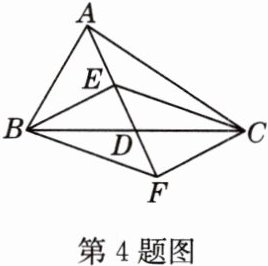

答案:
③
5 如图,在□ABCD中,对角线BD平分∠ABC,过点A作AE//BD,交CD的延长线于点E.
(1)求证:四边形ABCD是菱形.
(2)作EF⊥BC,交BC的延长线于点F,若∠ABC = 45°,BC = 2,求EF的长.
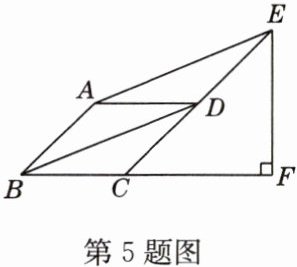
(1)求证:四边形ABCD是菱形.
(2)作EF⊥BC,交BC的延长线于点F,若∠ABC = 45°,BC = 2,求EF的长.

答案:
(1)证明:
∵四边形ABCD为平行四边形,
∴AD//BC,
∴∠ADB = ∠CBD.
∵BD平分∠ABC,
∴∠ABD = ∠CBD,
∴∠ADB = ∠ABD,
∴AB = AD,
∴平行四边形ABCD为菱形.(2)解:
∵四边形ABCD为菱形,
∴AB = BC = CD = 2.易证四边形ABDE为平行四边形,
∴DE = AB = 2,
∴CE = CD + DE = 2 + 2 = 4. 又CD//AB,
∴∠ECF = ∠ABC = 45°.
∵EF⊥BC,
∴∠F = 90°,
∴∠CEF = 45°,
∴CF = EF,由勾股定理得EF = 2√2.
∵四边形ABCD为平行四边形,
∴AD//BC,
∴∠ADB = ∠CBD.
∵BD平分∠ABC,
∴∠ABD = ∠CBD,
∴∠ADB = ∠ABD,
∴AB = AD,
∴平行四边形ABCD为菱形.(2)解:
∵四边形ABCD为菱形,
∴AB = BC = CD = 2.易证四边形ABDE为平行四边形,
∴DE = AB = 2,
∴CE = CD + DE = 2 + 2 = 4. 又CD//AB,
∴∠ECF = ∠ABC = 45°.
∵EF⊥BC,
∴∠F = 90°,
∴∠CEF = 45°,
∴CF = EF,由勾股定理得EF = 2√2.
6 能够判定一个四边形是菱形的条件是( )
A. 对角线相等且互相平分
B. 对角线相等且对角相等
C. 对角线互相垂直
D. 两组对角分别相等,且一条对角线平分一个内角
A. 对角线相等且互相平分
B. 对角线相等且对角相等
C. 对角线互相垂直
D. 两组对角分别相等,且一条对角线平分一个内角
答案:
D
7(易错题)如图,矩形ABCD的对角线AC,BD相交于点O,CE//BD,DE//AC,连接OE,则图中菱形的个数有 ( )
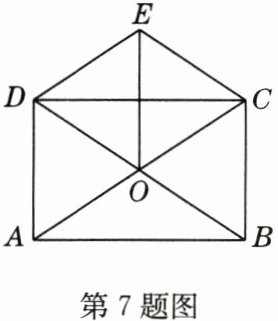
A. 0个
B. 1个
C. 2个
D. 3个

A. 0个
B. 1个
C. 2个
D. 3个
答案:
B 解析:四边形DOCE为菱形.
8 如图,在矩形ABCD中,AB = 4 cm,BC = 8 cm,点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P,Q的速度都是1 cm/s,设运动时间为t s. 则当t = ________s时,四边形AQCP是菱形.
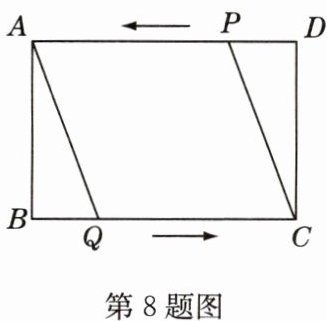

答案:
3 解析:易知四边形AQCP是平行四边形. 当AQ = CQ时,四边形AQCP是菱形.
∵BQ = t cm,
∴QC =(8 - t)cm. 在Rt△ABQ中,AQ² = AB² + BQ² = 4² + t²,CQ² =(8 - t)²,
∴4² + t² =(8 - t)²,解得t = 3.
∵BQ = t cm,
∴QC =(8 - t)cm. 在Rt△ABQ中,AQ² = AB² + BQ² = 4² + t²,CQ² =(8 - t)²,
∴4² + t² =(8 - t)²,解得t = 3.
查看更多完整答案,请扫码查看


