《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 计算：$(3\sqrt{2}-2\sqrt{3})(2\sqrt{3}+3\sqrt{2})=$________，$\frac{2}{3}\sqrt{\frac{5}{8}}\div\frac{1}{6}\sqrt{\frac{5}{2}}=$________．

答案： 6 2 解析： \[ \begin{aligned} &(3\sqrt{2}-2\sqrt{3})(2\sqrt{3}+3\sqrt{2})\\ =&(3\sqrt{2}-2\sqrt{3})(3\sqrt{2}+2\sqrt{3})\\ =&(3\sqrt{2})^{2}-(2\sqrt{3})^{2}\\ =&18 - 12\\ =&6 \end{aligned} \] \[ \begin{aligned} &\frac{2}{3}\sqrt{\frac{5}{8}}\div\frac{1}{6}\sqrt{\frac{5}{2}}\\ =&\frac{2}{3}\times6\sqrt{\frac{5}{8}\times\frac{2}{5}}\\ =&4\sqrt{\frac{1}{4}}\\ =&4\times\frac{1}{2}\\ =&2 \end{aligned} \]

2 计算：$(\sqrt{3}+2)^{2021}(\sqrt{3}-2)^{2022}=$________．

答案： $2-\sqrt{3}$ 解析： \[ \begin{aligned} &(\sqrt{3}+2)^{2021}(\sqrt{3}-2)^{2022}\\ =&[(\sqrt{3}+2)(\sqrt{3}-2)]^{2021}\cdot(\sqrt{3}-2)\\ =&(3 - 4)^{2021}\cdot(\sqrt{3}-2)\\ =&(-1)^{2021}\cdot(\sqrt{3}-2)\\ =&-(\sqrt{3}-2)\\ =&2-\sqrt{3} \end{aligned} \]

3 计算：
(1)$\sqrt{12}-\sqrt[3]{8}+|1 - \sqrt{3}|$；
(2)$\sqrt[3]{-8}+\sqrt{12}-9\sqrt{\frac{1}{3}}+(3\sqrt{2}+4)(3\sqrt{2}-4)$．

答案： 解：
(1) 原式$=2\sqrt{3}-2+\sqrt{3}-1 = 3\sqrt{3}-3$。
(2) 原式$=-2 + 2\sqrt{3}-9\times\frac{\sqrt{3}}{3}+(18 - 16)$ \[ \begin{aligned} &=-2 + 2\sqrt{3}-3\sqrt{3}+2\\ &=-\sqrt{3} \end{aligned} \]

4 (1)计算：$|2 - \sqrt{3}|+(2\sqrt{3})^{2}-(\sqrt{48}-\sqrt{\frac{1}{10}}\times\sqrt{30})$．
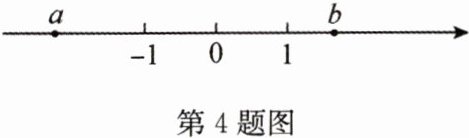
(2)实数$a$，$b$在数轴上对应点的位置如图所示，化简：$\sqrt{a^{2}}-\sqrt{b^{2}}+\sqrt{(a - b)^{2}}$．

答案： 解：
(1) 原式$=2-\sqrt{3}+12-(4\sqrt{3}-\sqrt{\frac{1}{10}\times30})$ \[ \begin{aligned} &=2-\sqrt{3}+12-4\sqrt{3}+\sqrt{3}\\ &=14 - 4\sqrt{3} \end{aligned} \]
(2) 由数轴知$a\lt -1$，$b\gt 1$， \[ \begin{aligned} &
\therefore原式=-a - b-(a - b)\\ &=-a - b - a + b\\ &=-2a \end{aligned} \]

5 已知$a = \sqrt{2}+1$，$b = \sqrt{2}-1$，则$a^{2}+b^{2}$的值为（ ）
A. $4\sqrt{2}$
B. $6$
C. $3 - 2\sqrt{2}$
D. $3 + 2\sqrt{2}$

答案： B 解析：当$a = \sqrt{2}+1$，$b = \sqrt{2}-1$时， \[ \begin{aligned} &原式=(\sqrt{2}+1)^{2}+(\sqrt{2}-1)^{2}\\ &=3 + 2\sqrt{2}+3 - 2\sqrt{2}\\ &=6 \end{aligned} \]

6 已知$x = \sqrt{5}-6$，则代数式$x^{2}+5x - 6$的值为（ ）
A. $2\sqrt{5}+3$
B. $5 - 5\sqrt{5}$
C. $3 - 2\sqrt{5}$
D. $5 - 7\sqrt{5}$

答案： D 解析：$\because x = \sqrt{5}-6$， \[ \begin{aligned} &
\therefore x^{2}+5x - 6\\ &=(\sqrt{5}-6)^{2}+5(\sqrt{5}-6)-6\\ &=5 + 36-12\sqrt{5}+5\sqrt{5}-30 - 6\\ &=5 - 7\sqrt{5} \end{aligned} \]

7 已知$\sqrt{a - 3}+\sqrt{2 - b}=0$，则$\frac{1}{\sqrt{a}}+\frac{\sqrt{6}}{\sqrt{b}}$的值为（ ）
A. $1$
B. $\sqrt{2}$
C. $\sqrt{3}$
D. $\frac{4\sqrt{3}}{3}$

答案： D 解析：$\because\sqrt{a - 3}+\sqrt{2 - b}=0$， $\therefore a - 3 = 0$，$2 - b = 0$， 解得$a = 3$，$b = 2$， \[ \begin{aligned} &
\therefore\frac{1}{\sqrt{a}}+\frac{\sqrt{6}}{\sqrt{b}}=\frac{1}{\sqrt{3}}+\frac{\sqrt{6}}{\sqrt{2}}=\frac{\sqrt{3}}{3}+\sqrt{3}=\frac{4\sqrt{3}}{3} \end{aligned} \]

8 若$a = \sqrt{3}-1$，求$a^{2}+2a + 2$的值．

答案： 解：$\because a = \sqrt{3}-1$，$(a + 1)^{2}=a^{2}+2a + 1$， \[ \begin{aligned} &
\therefore a^{2}+2a + 2\\ &=(a + 1)^{2}+1\\ &=(\sqrt{3}-1 + 1)^{2}+1\\ &=3 + 1\\ &=4 \end{aligned} \]