《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

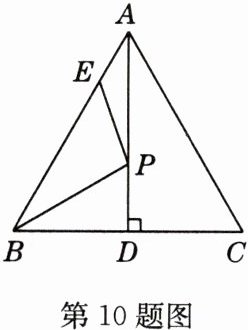
10 如图，AD为等边△ABC的边BC上的高，AB = 4，AE = 1，P为AD上一动点，则PE + PB的最小值为 （ ）

A.$2\sqrt{3}$
B.$\sqrt{13}$
C.$\sqrt{14}$
D.$\sqrt{15}$

答案： B 解析：$\because$点$B$、$C$关于直线$AD$对称，$\therefore$连接$CE$交$AD$于点$P$，此时$PE + PB$最小。作$EF \perp BC$于点$F$。$\because AB = 4$，$AE = 1$，$\therefore BE = 3$。又$\angle EBF = 60^{\circ}$，$\therefore \angle BEF = 30^{\circ}$，$\therefore BF = \frac{1}{2}BE = \frac{3}{2}$，$\therefore CF = CB - BF = 4 - \frac{3}{2} = \frac{5}{2}$。又$EF^2 = BE^2 - BF^2 = 3^2 - (\frac{3}{2})^2 = 9 - \frac{9}{4} = \frac{27}{4}$，$\therefore CE^2 = EF^2 + CF^2 = 13$，$\therefore CE = \sqrt{13}$。

11 若等边三角形的边长是a，则它的面积为_______.

答案： $\frac{\sqrt{3}}{4}a^2$ 解析：如图，在等边$\triangle ABC$中，作$AD \perp BC$于点$D$，则$BD = CD = \frac{a}{2}$。在$Rt\triangle ABD$中，$AB^2 = AD^2 + BD^2$，$\therefore AD^2 = AB^2 - BD^2 = a^2 - (\frac{a}{2})^2 = a^2 - \frac{1}{4}a^2 = \frac{3}{4}a^2$，$\therefore AD = \frac{\sqrt{3}}{2}a$，$\therefore S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = \frac{1}{2}a \cdot \frac{\sqrt{3}}{2}a = \frac{\sqrt{3}}{4}a^2$。

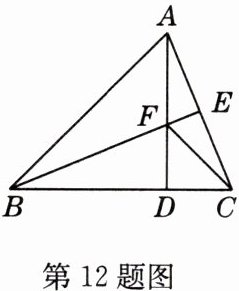
12 如图，在△ABC中，AB = BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD = 45°，AD与BE交于点F，连接CF.
(1)求证：BF = 2AE.
(2)若CD = $\sqrt{2}$，求AD的长.

答案： （1）证明：$\because AD \perp BC$，$\therefore \angle ADC = \angle BDF = 90^{\circ}$。又$\because \angle BAD = 45^{\circ}$，$\therefore AD = BD$。$\because BE \perp AC$，$AB = BC$，$\therefore AE = CE = \frac{1}{2}AC$，$\angle AEF = \angle BDF = 90^{\circ}$。又$\angle AFE = \angle DFB$，$\therefore \angle CAD = \angle DBF$。在$\triangle ADC$和$\triangle BDF$中，$\angle CAD = \angle FBD$，$AD = BD$，$\angle ADC = \angle BDF$，$\therefore \triangle ADC \cong \triangle BDF$，$\therefore AC = BF$，$\therefore BF = 2AE$。 （2）解：$\because \triangle ADC \cong \triangle BDF$，$\therefore CD = FD = \sqrt{2}$，由勾股定理，得$CF = 2$。$\because BE$垂直平分$AC$，$\therefore AF = CF = 2$，$\therefore AD = AF + FD = 2 + \sqrt{2}$。

13 (原创题)如图，在△ABC中，AC = BC，∠ACB = 90°，D是AB边上一点，且AD = 6，BD = 8，求CD的长.

答案： 解：作$CE \perp AB$于点$E$。$\because AC = BC$，$\therefore \angle ACE = \frac{1}{2}\angle ACB = \frac{1}{2} \times 90^{\circ} = 45^{\circ}$，且$AE = BE = \frac{1}{2}AB = \frac{1}{2} \times (AD + BD) = \frac{1}{2} \times (6 + 8) = \frac{1}{2} \times 14 = 7$，$\therefore DE = AE - AD = 7 - 6 = 1$。$\because \angle CEA = 90^{\circ}$，$\angle ACE = 45^{\circ}$，$\therefore \angle A = 45^{\circ}$，$\therefore \angle A = \angle ACE$，$\therefore CE = AE = 7$。在$Rt\triangle CED$中，$CD^2 = CE^2 + DE^2 = 7^2 + 1^2 = 50$，$\therefore CD = \sqrt{50} = 5\sqrt{2}$。

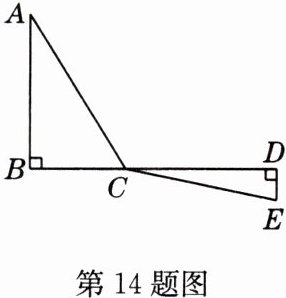
14 (探究题)如图，点C为线段BD上一动点，分别过点B、D作AB⊥BD，DE⊥BD，连接AC、EC，已知AB = 5，DE = 1，BD = 8，设BC = x.
(1)用含x的代数式表示AC + CE的长.
(2)请问：点C满足什么条件时，AC + CE最小？最小为多少？
(3)根据(2)中的规律和结论，请构图求代数式$\sqrt{x^{2}+4}+\sqrt{(12 - x)^{2}+9}$的最小值.

答案： 解：（1）由勾股定理，得$AC = \sqrt{AB^2 + BC^2} = \sqrt{5^2 + x^2} = \sqrt{x^2 + 25}$，$CE = \sqrt{DE^2 + DC^2} = \sqrt{1^2 + (8 - x)^2} = \sqrt{(8 - x)^2 + 1}$，$\therefore AC + CE = \sqrt{x^2 + 25} + \sqrt{(8 - x)^2 + 1}$。 （2）当点$A$、$C$、$E$在同一条直线上时，$AC + CE$的值最小，如图①。 平移线段$BD$，使$B$点与$A$点重合，$D$点的对应点是$F$，连接$DF$，则$AF = BD = 8$，$DF = AB = 5$，$\angle AFE = 90^{\circ}$。在$Rt\triangle AEF$中，$AE^2 = AF^2 + EF^2 = 8^2 + (5 + 1)^2 = 64 + 36 = 100$，$\therefore AE = 10$，$\therefore AC + CE$的最小值为10。 （3）如图②，$C$为线段$BD$上一点，$AB \perp BD$，$ED \perp BD$，且$AB = 2$，$DE = 3$，$BD = 12$，设$BC = x$，则$AC + EC = \sqrt{2^2 + x^2} + \sqrt{3^2 + (12 - x)^2} = \sqrt{x^2 + 4} + \sqrt{(12 - x)^2 + 9}$，当$A$、$C$、$E$在同一条直线上时，$\sqrt{x^2 + 4} + \sqrt{(12 - x)^2 + 9}$的值最小。同（2）道理一样可求得最小值为13。