《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

12 已知$a=\sqrt{5}+2,b=\sqrt{5}-2$，则二次根式$\sqrt{a^2+b^2+7}$的值为（ ）
A.$\sqrt{3}$
B.4
C.5
D.$\sqrt{5}$

答案： C 解析：$a + b=\sqrt{5}+2+\sqrt{5}-2=2\sqrt{5}$，$ab=(\sqrt{5}+2)\cdot(\sqrt{5}-2)=(\sqrt{5})^2-2^2=5 - 4=1$，$\therefore$原式$=\sqrt{a^2+2ab+b^2-2ab+7}=\sqrt{(a + b)^2-2ab+7}$ $=\sqrt{(2\sqrt{5})^2-2\times1+7}=\sqrt{20 - 2+7}=\sqrt{25}=5$

13 已知$m,n$是两个连续的自然数$(m ＜ n),q = mn,p=\sqrt{q + n}+\sqrt{q - m}$，则$p$（ ）
A.总是奇数
B.总是偶数
C.有时是奇数，有时是偶数
D.有时是有理数，有时是无理数

答案： A 解析：$p=\sqrt{mn + n}+\sqrt{mn - m}=\sqrt{n(m + 1)}+\sqrt{m(n - 1)}=\sqrt{n^2}+\sqrt{m^2}=n + m$ 设$m = a$，则$n = a + 1$， $\therefore p=a + 1+a=2a + 1$ $\therefore p$总是奇数。

14 若$0 ＜ a ＜ 1,a+\frac{1}{a}=6$，则代数式$\sqrt{a}-\frac{1}{\sqrt{a}}$的值为（ ）
A.±2
B.-2
C.±4
D.4

答案： B 解析：$(\sqrt{a}-\frac{1}{\sqrt{a}})^2=a-2+\frac{1}{a}=6 - 2=4$ $\because0 ＜ a ＜ 1,\therefore\sqrt{a}-\frac{1}{\sqrt{a}}＜0$ $\therefore\sqrt{a}-\frac{1}{\sqrt{a}}=-2$。故选B.

15 按如图所示的程序计算，若开始输入的$n$值为$\sqrt{2}$，则最后输出的结果是（ ）

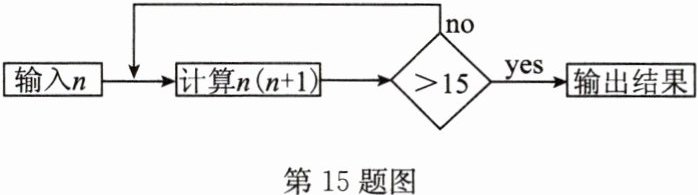
A.14
B.16
C.$8 + 5\sqrt{2}$
D.$14+\sqrt{2}$

答案： C

16 计算：$(\sqrt{3}+\sqrt{2})^2(\sqrt{3}-\sqrt{2})=$_______.

答案： $\sqrt{3}+\sqrt{2}$ 解析：原式$=(\sqrt{3}+\sqrt{2})[(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})]=(\sqrt{3}+\sqrt{2})[(\sqrt{3})^2-(\sqrt{2})^2]=(\sqrt{3}+\sqrt{2})(3 - 2)=\sqrt{3}+\sqrt{2}$

17 计算：$(\sqrt{7}+\sqrt{5})^4(\sqrt{7}-\sqrt{5})^4=$_______.

答案： 16 解析：原式$=[(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})]^4=[(\sqrt{7})^2-(\sqrt{5})^2]^4=(7 - 5)^4=2^4=16$

18 已知$3+\sqrt{2}$的小数部分与$3-\sqrt{2}$的小数部分分别为$a$和$b$，则$ab$的值为_______.

答案： $3\sqrt{2}-4$ 解析：由题知$a=\sqrt{2}-1$，$b=2-\sqrt{2}$， $\therefore ab=(\sqrt{2}-1)(2-\sqrt{2})=3\sqrt{2}-4$

19 解方程$\sqrt{3}(x + 1)=\sqrt{2}(x - 1)$，得$x=$_____.

答案： $-5 - 2\sqrt{6}$ 解析：$\sqrt{3}x+\sqrt{3}=\sqrt{2}x-\sqrt{2}$，即$(\sqrt{3}-\sqrt{2})x=-\sqrt{3}-\sqrt{2}$，$\therefore x=-5 - 2\sqrt{6}$

20 已知$a=\frac{2\sqrt{5}-3}{6},b=\frac{3 + 2\sqrt{5}}{6}$，求代数式$\sqrt{ab}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})$的值.

答案： 解：$\sqrt{ab}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})=\sqrt{ab}\cdot\sqrt{\frac{a}{b}}+\sqrt{ab}\cdot\sqrt{\frac{b}{a}}=\sqrt{a^2}+\sqrt{b^2}=|a|+|b|$ 由题设条件可知$a＞0,b＞0,\therefore$原式$=a + b=\frac{2\sqrt{5}-3}{6}+\frac{3 + 2\sqrt{5}}{6}=\frac{2\sqrt{5}-3+3 + 2\sqrt{5}}{6}=\frac{4\sqrt{5}}{6}=\frac{2\sqrt{5}}{3}$

22 (原创题)观察下列算式：
$\sqrt{4\times3\times2\times1 + 1}=\sqrt{25}=5$；①
$\sqrt{5\times4\times3\times2 + 1}=\sqrt{121}=11$；②
$\sqrt{6\times5\times4\times3 + 1}=\sqrt{361}=19$；③
$\sqrt{7\times6\times5\times4 + 1}=\sqrt{841}=29$；④
……
解答下列问题：
(1)用你发现的规律写出第⑥个等式.
(2)当$n=\sqrt{3}$时，求$\sqrt{(n + 3)(n + 2)(n + 1)n + 1}$的值.

答案： 解：（1）$\sqrt{9\times8\times7\times6 + 1}=\sqrt{3025}=55$ （2）$\sqrt{(n + 3)(n + 2)(n + 1)n+1}=(n + 3)n+1=n^2+3n + 1$ $\therefore$当$n=\sqrt{3}$时，原式$=(\sqrt{3})^2+3\times\sqrt{3}+1=4 + 3\sqrt{3}$