《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

12 直线$y = -x + 4$与$x$轴所夹的锐角的度数为（ ）
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D.以上均不正确

答案： B 解析：如图，设直线y = -x + 4与x轴、y轴的交点分别为A、B， 易求A点坐标为(4,0)，B点坐标为(0,4)，
∴OA = 4，OB = 4. 又
∵∠AOB = 90°，
∴∠BAO = 45°.

13 (易错题)经过点$A(4,0)$的直线与$y$轴交于点$B$，若$\triangle AOB$的面积为6，则直线$AB$的函数解析式为（ ）
A. $y = -\frac{3}{4}x + 3$
B. $y = \frac{3}{4}x + 3$
C. $y = -\frac{3}{4}x + 3或y = \frac{3}{4}x - 3$
D. $y = -\frac{4}{3}x + 3或y = \frac{4}{3}x + 3$

答案： C 解析：如图①，当点B在y轴正半轴上时，
∵$S_{\triangle AOB}=6$，
∴$\frac{1}{2}\cdot OA\cdot OB = 6$，即$\frac{1}{2}\times4OB = 6$，
∴OB = 3，
∴点B的坐标为(0,3)，故可求出直线AB的函数解析式为y = -$\frac{3}{4}$x + 3； 如图②，当点B在y轴负半轴上时，点B的坐标为(0,-3)，故可求出直线AB的函数解析式为y = $\frac{3}{4}$x - 3. 综上，直线AB的函数解析式为y = -$\frac{3}{4}$x + 3或y = $\frac{3}{4}$x - 3.

14 (经典题)一次函数$y = \frac{4}{3}x - b与y = \frac{4}{3}x - 1的图象之间的距离为3，则b的值为（ ）
A. -2或4
B. 2或-4
C. 4或-6
D. -4或6

答案： D 解析：如图①，当直线y = $\frac{4}{3}$x - b在直线y = $\frac{4}{3}$x - 1的下方时，设直线y = $\frac{4}{3}$x - 1与x轴，y轴分别交于点A，B. 求得点A的坐标为($\frac{3}{4}$,0)，点B的坐标为(0,-1). 设直线y = $\frac{4}{3}$x - b与y轴交于点C，则点C的坐标为(0,-b)，连接CA，作CD⊥AB于点D，又CD = 3，$AB=\sqrt{(\frac{3}{4})^2 + 1^2}=\frac{5}{4}$，BC = -1 - (-b) = b - 1，
∴$S_{\triangle ABC}=\frac{1}{2}\cdot BC\cdot OA=\frac{1}{2}(b - 1)\cdot\frac{3}{4}=\frac{3}{8}(b - 1)$. 又$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}\times\frac{5}{4}\times3=\frac{15}{8}$，
∴$\frac{3}{8}(b - 1)=\frac{15}{8}$，解得b = 6. 如图②，当直线y = $\frac{4}{3}$x - b在直线y = $\frac{4}{3}$x - 1的上方时，同理，可求得b = -4. 故选D. 方法总结：在解决一次函数的题目时要善于利用三角形的面积来解决问题.

15 已知一次函数$y = kx + b$,当1≤x≤4时,3≤y≤6,则$\frac{b}{k}$的值是________.

答案： 2或 -7

16 (原创题)如图，Rt$\triangle ABC$的锐角顶点在x轴上，直角顶点C在y轴负半轴上.若A、C两点的坐标分别为(3,0)、(0,-4)，则直线BC的函数解析式为__________.

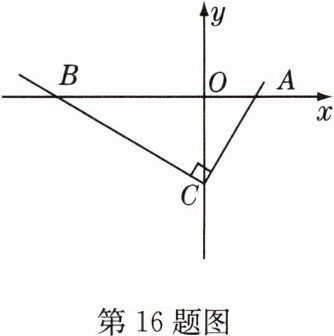
答案： y = -$\frac{3}{4}$x - 4 解析：由A(3,0)，C(0,-4)，易得AO = 3，CO = 4，AC = 5. 设点B的坐标为(m,0)，则OB = -m，AB = 3 - m. 在Rt△BOC中，$BC^2 = BO^2 + CO^2 = (-m)^2 + 4^2$，在Rt△BCA中，$BC^2 = AB^2 - AC^2 = (3 - m)^2 - 5^2$，
∴$(-m)^2 + 4^2 = (3 - m)^2 - 5^2$，解得m = -$\frac{16}{3}$，
∴点B的坐标为(-$\frac{16}{3}$,0). 根据B、C两点的坐标可求出直线BC的函数解析式为y = -$\frac{3}{4}$x - 4.

17 如图，直线$y = -\frac{4}{3}x + 8与x轴、y轴分别相交于点A、B$.设M是OB上一点，若将$\triangle ABM沿AM折叠使点B恰好落在x轴上点B'处.求：

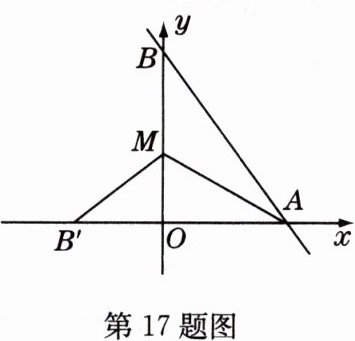
(1)点B'的坐标；
(2)直线AM的函数解析式.

答案： 解：
(1)把y = 0代入y = -$\frac{4}{3}$x + 8，解得x = 6，
∴点A的坐标为(6,0). 把x = 0代入y = -$\frac{4}{3}$x + 8，解得y = 8，
∴点B的坐标为(0,8)，
∴$AB=\sqrt{OA^2 + OB^2}=\sqrt{6^2 + 8^2}=10$. 又△AMB≌△AMB'，
∴AB' = AB = 10. 又OA = 6，
∴OB' = 4，
∴点B'的坐标为(-4,0).
(2)设直线AM的解析式为y = kx + b(k≠0)，点M的坐标为(0,m)，则MO = m，BM = B'M = 8 - m. 在Rt△MOB'中，$OM^2 + OB'^2 = MB'^2$，即$m^2 + 4^2 = (8 - m)^2$，解得m = 3.
∴点M的坐标为(0,3). 把点A(6,0)和点M(0,3)代入y = kx + b(k≠0)，解得k = -$\frac{1}{2}$，b = 3，
∴直线AM的函数解析式为y = -$\frac{1}{2}$x + 3.

18 在平面直角坐标系xOy中，直线y = 2x + m与y轴交于点A，与直线y = -x + 4交于点B(3,n)，P为直线y = -x + 4上一点.
(1)求m,n的值.
(2)在平面直角坐标系xOy中，画出直线y = 2x + m和y = -x + 4的图象.
(3)当线段AP最短时，求点P的坐标.

答案： 解：
(1)把点B(3,n)代入y = -x + 4，得n = -3 + 4，
∴n = 1，
∴点B的坐标为(3,1). 把点B(3,1)代入y = 2x + m，得1 = 6 + m，
∴m = -5. 综上，m = -5，n = 1.
(2)
∵m = -5，
∴画出图象如图①所示.
(3)如图②，当AP垂直于直线y = -x + 4时，线段AP最短，过点P作PQ⊥y轴于点Q，设P点坐标为(a,-a + 4)，则Q点坐标为(0,-a + 4). 设直线y = -x + 4与x轴的交点为D，易求点D的坐标为(4,0)，
∴OC = OD = 4，
∴△COD为等腰直角三角形.
∵OD//PQ，
∴∠CPQ = 45°. 又∠CPA = 90°，
∴∠QPA = 45°. 又∠PQA = 90°，
∴∠QAP = 45°，
∴∠QPA = ∠QAP，
∴QA = QP. 又QP = a，QA = -a + 4 - (-5) = 9 - a，
∴a = 9 - a，2a = 9，解得a = $\frac{9}{2}$， -a + 4 = -$\frac{9}{2}$ + 4 = -$\frac{1}{2}$，
∴点P的坐标为($\frac{9}{2}$,-$\frac{1}{2}$). 方法总结：当直线y = kx + b中k的值为1或 -1时，这条直线与x轴的夹角为45°，即直线y = kx + b与两坐标轴的交点及原点构成等腰直角三角形.