《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 下列说法正确的是 （ ）
A. 已知a,b,c是三角形的三边长，则$a^{2}+b^{2}=c^{2}$
B. 在直角三角形中，两边的平方和等于第三边的平方
C. 在Rt△ABC中，∠C = 90°，a,b,c分别是∠A，∠B，∠C所对的边，所以$a^{2}+b^{2}=c^{2}$
D. 在Rt△ABC中，∠B = 90°，a,b,c分别是∠A，∠B，∠C所对的边，所以$a^{2}+b^{2}=c^{2}$

答案： C

2 如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积分别为$S_{1}=\frac{25}{8}\pi$，$S_{2}=2\pi$，则$S_{3}$等于_______.

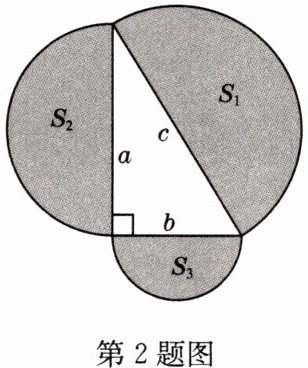
答案： $\frac{9}{8}\pi$ 解析：由圆的面积公式，得$S_1 = \frac{1}{2}\pi \cdot (\frac{c}{2})^2 = \frac{25}{8}\pi$，$S_2 = \frac{1}{2}\pi \cdot (\frac{a}{2})^2 = 2\pi$，解得$c^2 = 25$，$a^2 = 16$。根据勾股定理，得$b^2 = c^2 - a^2 = 9$。故$S_3 = \frac{1}{2}\pi \cdot (\frac{b}{2})^2 = \frac{1}{8}\pi b^2 = \frac{9}{8}\pi$。

3 已知直角三角形的两条直角边长分别为5和12，则斜边长为 （ ）
A. 7
B. 17
C. 13
D. 23

答案： C

4 在Rt△ABC中，∠C = 90°，若AB = $2\sqrt{3}$，AC = 3，则BC = （ ）
A.$\sqrt{3}$
B. 3
C. 6
D.$\sqrt{6}$

答案： A

5 在Rt△ABC中，∠C = 90°，∠A = 30°，若AC = $\sqrt{6}$，则AB = _______.

答案： $2\sqrt{2}$

6 已知在锐角△ABC中，AB = AC = 10，BD⊥AC于点D，CD = 2，则BC的长是_______.

答案： $2\sqrt{10}$ 解析：$\because AB = AC = 10$，$CD = 2$，$\therefore AD = 8$。$\because BD \perp AC$于点$D$，$\therefore \angle ADB = 90^{\circ}$，$\therefore BD^2 = AB^2 - AD^2 = 36$，$\therefore BC = \sqrt{BD^2 + CD^2} = \sqrt{36 + 4} = 2\sqrt{10}$。

7 (易错题)直角三角形的三边长分别为3、4、x，则x的可能值有 （ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： B 解析：3只能是直角边长，4可能是直角边长，也可能是斜边长，故$x$的可能值有2个。

8 (2022·南充)如图，在Rt△ABC中，∠C = 90°，∠BAC的平分线交BC于点D，DE//AB，交AC于点E，DF⊥AB于点F，DE = 5，DF = 3，则下列结论错误的是 （ ）

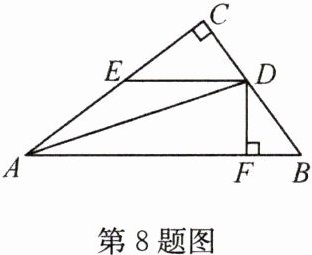
A. BF = 1
B. DC = 3
C. AE = 5
D. AC = 9

答案： A 解析：$\because AD$平分$\angle BAC$，$\angle C = 90^{\circ}$，$DF \perp AB$，$\therefore \angle 1 = \angle 2$，$DC = FD$，$\angle C = \angle DFB = 90^{\circ}$，$\because DE // AB$，$\therefore \angle 2 = \angle 3$，$\therefore \angle 1 = \angle 3$，$\therefore AE = DE$，$\because DE = 5$，$DF = 3$，$\therefore AE = 5$，$CD = 3$，故选项B、C正确；$\therefore CE = \sqrt{DE^2 - CD^2} = 4$，$\therefore AC = AE + EC = 5 + 4 = 9$，故选项D正确。故选A。

9 (经典题)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若$(a + b)^{2}=21$，大正方形的面积为13，则小正方形的面积为 （ ）

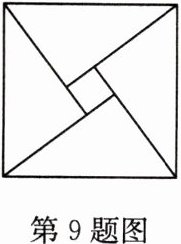
A. 3
B. 4
C. 5
D. 6

答案： C 解析：$\because (a + b)^2 = 21$，$\therefore a^2 + 2ab + b^2 = 21$。$\because$大正方形的面积为13，$\therefore a^2 + b^2 = 13$，$\therefore 2ab = 21 - 13 = 8$，即4个直角三角形的面积和为8，$\therefore$小正方形的面积为13 - 8 = 5。故选C。