《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

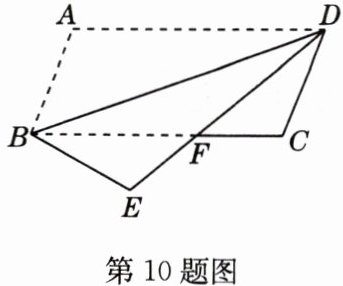
10 如图，将□ABCD沿对角线BD折叠，使点A落在点E处，DE交BC于点F，若∠ABD = 48°，∠CFD = 40°，则∠E为 （ ）

A. 102°
B. 112°
C. 122°
D. 92°

答案： B

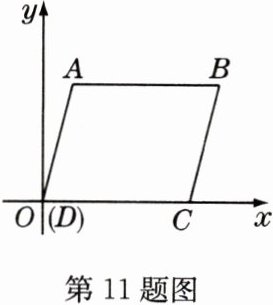
11 如图，在平面直角坐标系中，已知□ABCD的顶点A(1,4)、C(5,0)，则顶点B的坐标为 （ ）

A. (5,4)
B. (6,4)
C. (6,5)
D. (5,6)

答案： B

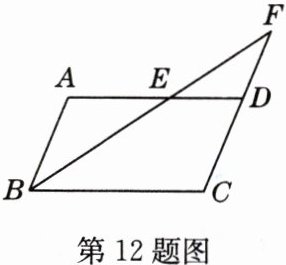
12 如图，在□ABCD中，AB = 4 cm，AD = 7 cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF = （ ）

A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm

答案： B 解析：
∵四边形ABCD为平行四边形，
∴AD//BC，
∴∠AEB = ∠CBE.
∵BE平分∠ABC，
∴∠ABE = ∠CBE，
∴∠ABE = ∠AEB，
∴AE = AB = 4 cm. 又AD = 7 cm，
∴DE = 3 cm.
∵AB//CD，
∴∠F = ∠ABE = ∠AEB = ∠DEF，
∴DF = DE = 3 cm. 名师点睛：平行四边形内角的平分线，把平行四边形分割成一个等腰三角形和一个梯形. 如图，若AE平分∠BAD，则△ADE为等腰三角形

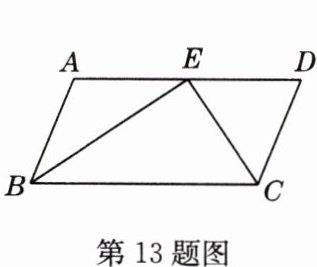
13 如图，在□ABCD中，BE、CE分别平分∠ABC和∠BCD，若AB = 5，BE = 8，则CE的长为 ________．

答案： 6

14 如图，在□ABCD中，DE = CE，连接AE并延长交BC的延长线于点F．
(1)求证：△ADE≌△FCE.
(2)若AB = 2BC，∠F = 30°，求∠B的度数.

答案： （1）证明：
∵四边形ABCD为平行四边形，
∴AD//BC，
∴∠DAE = ∠F. 又DE = CE，∠AED = ∠FEC，
∴△ADE≌△FCE(AAS). （2）解：
∵AB = 2BC，BC = AD = CF，
∴AB = FB，
∴∠F = ∠BAF = 30°，
∴∠B = 180° - 2×30° = 120°.

15 在□ABCD中，AB = 6，AD = 8，∠B = 45°，则□ABCD的面积为 ________．

答案： 24√2 解析：作AE⊥BC于点E. 在Rt△ABE中，
∵∠B = 45°，∠AEB = 90°，
∴∠BAE = 45°，
∴AE = BE. 又AB = 6，由勾股定理可求AE = 3√2.
∴S□ABCD = BC·AE = 8×3√2 = 24√2.

16 如图，点E在□ABCD内，AF//BE，DF//CE.
(1)求证：△BCE≌△ADF.
(2)设□ABCD的面积为S，四边形AEDF的面积为T，求$\frac{S}{T}$的值.

答案： （1）证明：延长BA到点G，如图.
∵四边形ABCD为平行四边形，
∴AD//BC，
∴∠GAD = ∠GBC.
∵AF//BE，
∴∠GAF = ∠GBE，
∴∠FAD = ∠EBC. 同理，∠FDA = ∠ECB. 又AD = BC，
∴△BCE≌△ADF. （2）解：
∵△BCE≌△ADF，
∴S△BCE = S△ADF. 又S△BCE + S△ADE = 1/2 S□ABCD，
∴S△ADF + S△ADE = 1/2 S□ABCD，即S四边形AEDF = 1/2 S□ABCD，即S/T = 2/1 = 2.