《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

10 如图，在菱形ABCD中，已知∠BAD = 80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF =（ ）

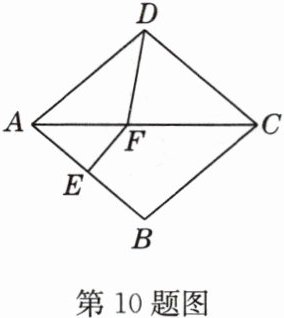
A. 50°
B. 60°
C. 70°
D. 80° 

答案： B 解析：连接FB.
∵四边形ABCD为菱形，
∴∠BAF = ∠DAF = $\frac{1}{2}$×80° = 40°. 又
∵AD = CD，
∴∠DAF = ∠DCF = 40°，
∴∠ADC = 180° - 2×40° = 100°.
∵EF垂直平分AB，
∴FA = FB，
∴∠ABF = ∠BAF = 40°. 易证△ADF≌△ABF，
∴∠ADF = ∠ABF = 40°，
∴∠CDF = 100° - 40° = 60°.技巧规律：菱形对角线上的一点与其他两个顶点的连线把菱形分割成两对全等的三角形. 如图，△ABP≌△CBP，△ADP≌△CDP

11 如图，在菱形ABCD中，∠A = 60°，AB = 2，E，F两点分别从A，B两点同时出发，以相同的速度分别向终点B，C移动，连接EF，在移动过程中，EF的最小值为（ ）

A. 1
B. $\sqrt{2}$
C. $\frac{3}{2}$
D. $\sqrt{3}$

答案： D 解析：连接BD.
∵四边形ABCD为菱形，
∴AB = AD. 又
∵∠A = 60°，
∴△ABD为等边三角形，
∴BD = AD，∠DBA = 60°. 又∠ABC = 120°，
∴∠DBF = 60°.在△ADE和△BDF中，AD = BD，∠A = ∠DBF，AE = BF，
∴△ADE≌△BDF，
∴DE = DF，∠ADE = ∠BDF. 又∠ADE + ∠EDB = 60°，
∴∠BDF + ∠EDB = 60°，
∴∠EDF = 60°，
∴△DEF为等边三角形，
∴EF = DE. 当DE⊥AB时，DE有最小值. 此时，DE = $\sqrt{3}$，
∴EF的最小值为$\sqrt{3}$.技巧规律：当菱形中有一个角为60°时，连接较短的对角线，可以把菱形分成两个等边三角形.

12 如图，在菱形ABCD中，AB = 2，∠A = 60°，将菱形ABCD翻折，使点A落在CD的中点E处，折痕为FG，则EF的长为（ ）

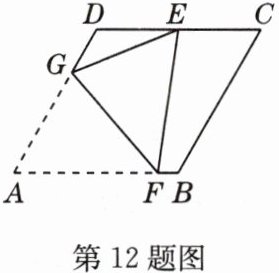
A. $\frac{7}{4}$
B. $\frac{9}{5}$
C. $\frac{19}{10}$
D. $\frac{7\sqrt{3}}{6}$ 

答案： A 解析：连接BE. 由∠A = ∠C = 60°，E为CD中点，易证得BE⊥CD. 又AB//CD，
∴EB⊥AB，
∴∠EBF = 90°，且BE = $\sqrt{3}$. 设AF = EF = x，则BF = 2 - x.在Rt△BEF中，BF² + BE² = EF²，
∴(2 - x)² + ($\sqrt{3}$)² = x²，解得x = $\frac{7}{4}$，
∴EF = $\frac{7}{4}$.

13 如图，在线段AB上取一点C，分别以AC，BC为边作菱形ACDE和菱形BCFG，使点D在CF上，连接EG，H是EG的中点，EG = 4，连接CH，则CH的长是________．

答案： 2 解析：如图，连接CE，CG.
∵四边形ACDE和四边形BCFG均为菱形，
∴CE平分∠ACD，CG平分∠BCF，
∴∠ECG = 90°. 又H为EG中点，
∴CH = $\frac{1}{2}$EG = $\frac{1}{2}$×4 = 2.

14 如图，在菱形ABCD中，对角线AC，BD相交于点O，AB = 5，AC = 6，过点D作AC的平行线交BC的延长线于点E，则△BDE的面积为________．

答案： 24

15 如图，在菱形ABCD中，E，F分别是边BC，CD的中点，EG⊥AD于点G，连接GF，若∠A = 80°，则∠DGF的度数为________．

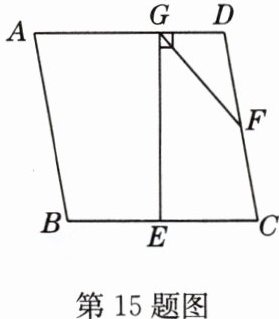
答案： 50° 解析：延长GF交BC的延长线于点H. 易证△CFH≌△DFG，
∴HF = GF，∠H = ∠DGF.
∵GE⊥AD，
∴GE⊥BC，
∴∠GEH = 90°. 连接EF.
∵E、F分别为BC、CD中点，BC = DC，
∴CE = CF. 又∠BCD = ∠A = 80°，
∴∠CEF = $\frac{180° - 80°}{2}$ = 50°.
∵在Rt△GEH中，GF = HF，
∴EF = $\frac{1}{2}$GH = HF，
∴∠H = ∠CEF = 50°，
∴∠DGF = 50°.名师点睛：中点遇平行，一定证全等，这种方法在平行四边形中经常用到，我们要熟记在心.

16 (2022·大连)如图，四边形ABCD是菱形，点E，F分别在AB，AD上，AE = AF.求证：CE = CF. [img id=第16题图]

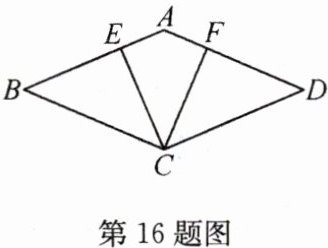
答案： 证明：
∵四边形ABCD是菱形，
∴AB = AD = BC = DC，∠B = ∠D，
∵AE = AF，
∴AB - AE = AD - AF，
∴BE = DF，在△BCE和△DCF中，$\begin{cases}BE = DF\\\angle B = \angle D\\BC = DC\end{cases}$，
∴△BCE≌△DCF(SAS)，
∴CE = CF.

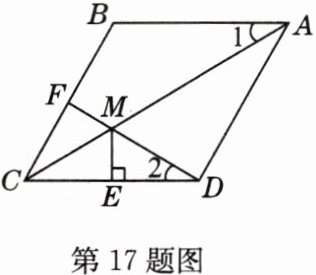
17 如图，已知在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1 = ∠2.
(1)若CE = 1,求BC的长.
(2)求证:AM = DF + ME. 

答案：
(1)解：
∵四边形ABCD是菱形，
∴BC = CD，AB//CD，
∴∠1 = ∠DCA.
∵∠1 = ∠2，
∴∠2 = ∠DCA，
∴DM = CM.
∵ME⊥CD，CE = 1，
∴CD = 2CE = 2，
∴BC = CD = 2.
(2)证明：设AB与DF的延长线相交于点G.
∵F为BC的中点，
∴BC = 2CF = 2BF.
∵CD = 2CE，BC = CD，
∴CE = CF，
∵四边形ABCD是菱形，
∴∠ECM = ∠FCM.又CM = CM，CE = CF，
∴△CEM≌△CFM，
∴ME = MF.
∵四边形ABCD是菱形，
∴AB//CD，
∴∠2 = ∠G.又
∵∠DFC = ∠GFB，CF = BF，
∴△DCF≌△GBF，
∴DF = GF.
∵∠2 = ∠G，∠1 = ∠2，
∴∠1 = ∠G，
∴AM = GM.又
∵MG = GF + MF，DF = GF，ME = MF，
∴AM = DF + ME.