《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 化简$(-\sqrt{7})^{2}$的结果为 （ ）
A. -7
B. 7
C. -49
D. 49

答案： B

2 化简$\sqrt{(-10)^{2}}$的结果为 （ ）
A. -10
B. 10
C. -100
D. 100

答案： B

3 计算$\sqrt{3^{-2}}$得 （ ）
A. 3
B. -3
C. $\frac{1}{3}$
D. $-\frac{1}{3}$

答案： C 解析：$\sqrt{3^{-2}}=\sqrt{\frac{1}{3^{2}}}=\sqrt{\frac{1}{9}}=\frac{1}{3}$。

4 当$x\leqslant3$时，化简$\sqrt{x^{2}-6x + 9}=$ （ ）
A. $x - 3$
B. $3 - x$
C. $x + 3$
D. $-x - 3$

答案： B 解析：$\sqrt{x^{2}-6x + 9}=\sqrt{(x - 3)^{2}}=\vert x - 3\vert$。$\because x\leq3$，$\therefore x - 3\leq0$，$\therefore$原式$=-(x - 3)=3 - x$。注意：当$a\lt0$时，$\sqrt{a^{2}}=-a$。

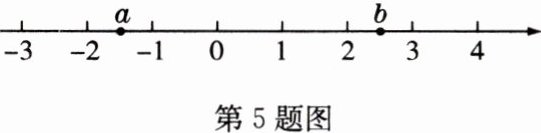
5 (易错题)实数$a,b$在数轴上的位置如图所示，则化简$\sqrt{a^{2}}+\sqrt{b^{2}}-\sqrt{(a - b)^{2}}$的结果是（ ）

A. 0
B. $-2a$
C. $2b$
D. $-2a + b$

答案： A 解析：由题图可知$a\lt0$，$b\gt0$，$a\lt b$，$\therefore$原式$=\vert a\vert+\vert b\vert-\vert a - b\vert=-a + b + a - b = 0$。

6 (易错题)化简$\sqrt{a^{6}}$得 （ ）
A. $a^{2}$
B. $a^{3}$
C. $a^{2}$或$-a^{2}$
D. $a^{3}$或$-a^{3}$

答案： D 解析：$\sqrt{a^{6}}=\sqrt{(a^{3})^{2}}=\vert a^{3}\vert$，当$a\geq0$时，原式$=a^{3}$，当$a\lt0$时，原式$=-a^{3}$。

7 若$\sqrt{(a - 3)^{2}} = 3 - a$，则$a$与3的大小关系是（ ）
A. $a ＜ 3$
B. $a\leqslant3$
C. $a ＞ 3$
D. $a\geqslant3$

答案： B 解析：由题意得$\sqrt{(a - 3)^{2}}=\vert a - 3\vert=3 - a$，$\therefore a - 3\leq0$，$\therefore a\leq3$。故选B。

8 若$\sqrt{a^{2}} = 4$，则$a =$_______.

答案： $\pm4$ 解析：$\because\sqrt{4^{2}} = 4$，$\sqrt{(-4)^{2}}=\vert - 4\vert = 4$，$\therefore a = 4$或$a = - 4$。

9 若$a = 2\sqrt{3},b = 3\sqrt{2}$，则$a^{2}-b^{2}=$_______.

答案： $-6$ 解析：$a^{2}-b^{2}=(2\sqrt{3})^{2}-(3\sqrt{2})^{2}=12 - 18=-6$。

10 计算：$(x\sqrt{x})^{2}=$_______.

答案： $x^{3}$ 解析：$(x\sqrt{x})^{2}=x^{2}\cdot(\sqrt{x})^{2}=x^{2}\cdot x = x^{3}$。

11 下列各式正确的是（ ）
A. $(-\sqrt{5})^{2} = -5$
B. $\sqrt{(-0.5)^{2}} = -0.5$
C. $(-\sqrt{5})^{2} = 5^{2}$
D. $\sqrt{(-0.5)^{2}} = 0.5$

答案： D

12 设$n$为正整数，且$n ＜ \sqrt{65} ＜ n + 1$，则$n$的值为（ ）
A. 5
B. 6
C. 7
D. 8

答案： D

13 已知$\sqrt{12 - n}$是正整数，则实数$n$的最大值为（ ）
A. 12
B. 11
C. 8
D. 3

答案： B

14 已知$\triangle ABC$的三边长分别为$a,1,3$，则化简$|9 - 2a|-\sqrt{9 - 12a + 4a^{2}}$的结果是（ ）
A. $12 - 4a$
B. $4a - 12$
C. 12
D. -12

答案： A 解析：由题意可得$2\lt a\lt4$，$\therefore4\lt2a\lt8$。原式$=\vert9 - 2a\vert-\sqrt{(3 - 2a)^{2}}=\vert9 - 2a\vert-\vert3 - 2a\vert=9 - 2a-(2a - 3)=9 - 2a - 2a + 3=12 - 4a$。

15 若$\sqrt{x^{2}-2x + 1}-\sqrt{x^{2}-4x + 4} = 1$，则$x$的取值范围为（ ）
A. $x\geqslant0$
B. $x\leqslant1$
C. $1\leqslant x\leqslant2$
D. $x\geqslant2$

答案： D

16 (经典题)若$\sqrt{a^{2}}+a = 0$，则$a$的取值范围是（ ）
A. $a\geqslant0$
B. $a\leqslant0$
C. $a = 0$
D. $a\neq0$

答案： B 解析：$\because\sqrt{a^{2}}+a=\vert a\vert+a = 0$，$\therefore a\leq0$。故选B。名师点睛：本题考查的是二次根式的化简，掌握二次根式的性质$\sqrt{a^{2}}=\vert a\vert$是解题的关键。

17 如果$x ＜ -4$，那么$|(2 - x)-\sqrt{(2 + x)^{2}}|$的值为_______.

答案： 4 解析：$\because x\lt - 4$，$\therefore\vert2 - x-\sqrt{(2 + x)^{2}}\vert=\vert2 - x + 2 + x\vert = 4$。

18 化简：$(\sqrt{2 - x})^{2}+\sqrt{(x - 3)^{2}}=$_______.

答案： $5 - 2x$ 解析：由$\sqrt{2 - x}$可知$2 - x\geq0$，$\therefore x\leq2$。$\therefore x - 3\lt0$，$\therefore$原式$=2 - x + 3 - x = 5 - 2x$。

19 比较大小：$3\sqrt{5}$_______$5\sqrt{3}$.

答案： $\lt$ 解析：$3\sqrt{5}=\sqrt{9\times5}=\sqrt{45}$，$5\sqrt{3}=\sqrt{25\times3}=\sqrt{75}$，$\therefore3\sqrt{5}\lt5\sqrt{3}$。

20 当$a ＜0$时，化简：$|a-\sqrt{a^{2}}|=$_______.

答案： $-2a$ 解析：$\vert a-\sqrt{a^{2}}\vert=\vert a-\vert a\vert\vert=\vert a + a\vert=\vert2a\vert=-2a$。

21已知$x ＜3,y=\frac{\sqrt{x^{2}-6x +9}}{x -3}-3$，则$\sqrt{y^{2}}=$_______.

答案： 4 解析：$y=\frac{\sqrt{(x - 3)^{2}}}{x - 3}-3=\frac{\vert x - 3\vert}{x - 3}-3=\frac{3 - x}{x - 3}-3=-1 - 3=-4$。$\therefore\sqrt{y^{2}}=\sqrt{(-4)^{2}} = 4$。