《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

9 已知$a = \sqrt{2020}-\sqrt{2019}$，$b = \sqrt{2021}-\sqrt{2020}$，$c = \sqrt{2022}-\sqrt{2021}$，则下列结论中正确的是（ ）
A. $a＞b＞c$
B. $c＞b＞a$
C. $b＞a＞c$
D. $b＞c＞a$

答案： A 解析：$\frac{1}{a}=\frac{1}{\sqrt{2020}-\sqrt{2019}}=\sqrt{2020}+\sqrt{2019}$，$\frac{1}{b}=\frac{1}{\sqrt{2021}-\sqrt{2020}}=\sqrt{2021}+\sqrt{2020}$，$\frac{1}{c}=\frac{1}{\sqrt{2022}-\sqrt{2021}}=\sqrt{2022}+\sqrt{2021}$。 $\because0\lt\frac{1}{a}\lt\frac{1}{b}\lt\frac{1}{c}$，$\therefore a\gt b\gt c$。

10 比较大小：(1)$\sqrt{11}-\sqrt{3}$与$\sqrt{10}-2$；(2)$2\sqrt{2}-\sqrt{5}$与$\sqrt{10}-\sqrt{7}$．

答案： 解：
(1) $(\sqrt{11}-\sqrt{3})^{2}=11-2\times\sqrt{11}\times\sqrt{3}+3 = 14-2\sqrt{33}$， $(\sqrt{10}-2)^{2}=10-2\times\sqrt{10}\times2 + 4 = 14-2\sqrt{40}$。 $\because33\lt40$，$\therefore2\sqrt{33}\lt2\sqrt{40}$， $\therefore14-2\sqrt{33}\gt14-2\sqrt{40}$，$\therefore(\sqrt{11}-\sqrt{3})^{2}\gt(\sqrt{10}-2)^{2}$。 又$\because\sqrt{11}-\sqrt{3}\gt0$，$\sqrt{10}-2\gt0$，$\therefore\sqrt{11}-\sqrt{3}\gt\sqrt{10}-2$。
(2) $\frac{1}{2\sqrt{2}-\sqrt{5}}=\frac{2\sqrt{2}+\sqrt{5}}{(2\sqrt{2}-\sqrt{5})(2\sqrt{2}+\sqrt{5})}=\frac{2\sqrt{2}+\sqrt{5}}{3}$， $\frac{1}{\sqrt{10}-\sqrt{7}}=\frac{\sqrt{10}+\sqrt{7}}{(\sqrt{10}-\sqrt{7})(\sqrt{10}+\sqrt{7})}=\frac{\sqrt{10}+\sqrt{7}}{3}$。 $\because\frac{2\sqrt{2}+\sqrt{5}}{3}=\frac{\sqrt{8}+\sqrt{5}}{3}\lt\frac{\sqrt{10}+\sqrt{7}}{3}$， $\therefore\frac{1}{2\sqrt{2}-\sqrt{5}}\lt\frac{1}{\sqrt{10}-\sqrt{7}}$， $\therefore2\sqrt{2}-\sqrt{5}\gt\sqrt{10}-\sqrt{7}$。

11 现将某一长方形纸片的长增加$3\sqrt{2}\text{ cm}$，宽增加$6\sqrt{2}\text{ cm}$，就成为一个面积为$128\text{ cm}^{2}$的正方形纸片，则原长方形纸片的面积为（ ）
A. $18\text{ cm}^{2}$
B. $20\text{ cm}^{2}$
C. $36\text{ cm}^{2}$
D. $48\text{ cm}^{2}$

答案： B 解析：$\because$面积为$128\ cm^{2}$的正方形纸片的边长为$8\sqrt{2}\ cm$， $\therefore$原长方形纸片的长为$8\sqrt{2}-3\sqrt{2}=5\sqrt{2}(cm)$，宽为$8\sqrt{2}-6\sqrt{2}=2\sqrt{2}(cm)$， $\therefore$原长方形纸片的面积为$5\sqrt{2}\times2\sqrt{2}=20(cm^{2})$。

12 如图，在长方形内有两个相邻的正方形$A$，$B$，正方形$A$的面积为$2$，正方形$B$的面积为$4$，则图中阴影部分的面积是________．

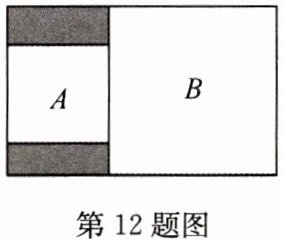
答案： $2\sqrt{2}-2$ 解析：设正方形$A$，$B$的边长分别是$x$，$y(x\lt y)$， 则$x^{2}=2$，$y^{2}=4$， $\therefore x=\sqrt{2}$，$y = 2$， 则阴影部分的面积是$(y - x)x=(2-\sqrt{2})\times\sqrt{2}=2\sqrt{2}-2$。

13 (探究题)在数学课上，老师出了一道题：化简$\sqrt{(1 - \sqrt{2})^{2}}$．同学们马上举手发言，小明站起来说：“老师，这道题太简单了，因为平方与开平方互为逆运算，所以$\sqrt{(1 - \sqrt{2})^{2}}=1 - \sqrt{2}$．”而老师却说小明错了，为什么呢？这是因为如果$\sqrt{a^{2}}=a$成立，必须具备条件$a\geq0$，而$1 - \sqrt{2}＜0$．正确的思路是先判断正负，然后开方．所以$\sqrt{(1 - \sqrt{2})^{2}}=\sqrt{2}-1$，你看明白了吗？请你做一做下面的习题：
(1)化简：$\sqrt{(\sqrt{2}-\sqrt{3})^{2}}=$________．
(2)化简：$\sqrt{(1 - \sqrt{2})^{2}}+\sqrt{(\sqrt{2}-\sqrt{3})^{2}}+\sqrt{(\sqrt{3}-\sqrt{4})^{2}}+\cdots+\sqrt{(\sqrt{2021}-\sqrt{2022})^{2}}$．
(3)已知$a$，$b$，$c$是三角形的三边长，化简：$\sqrt{(a + b - c)^{2}}+\sqrt{(b - c - a)^{2}}$．

答案： 解：
(1) $\sqrt{3}-\sqrt{2}$
(2) 原式$=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\cdots+\sqrt{2022}-\sqrt{2021}=\sqrt{2022}-1$。
(3) 原式$=a + b - c+(a + c - b)=a + b - c+a + c - b = 2a$。