第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
10 (易错题)如图,在正方形ABCD中,正方形的面积为2,G是AD边上一点,AG = 1,以AG为边作正方形AGEF,则∠AEB为 ( )
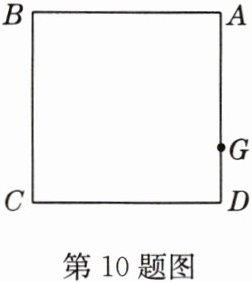
A. 45°
B. 22.5°
C. 45°或22.5°
D. 67.5°或22.5°

A. 45°
B. 22.5°
C. 45°或22.5°
D. 67.5°或22.5°
答案:
D 解析:如图①,当正方形AGEF在正方形ABCD外部时,由正方形ABCD的面积为2,可得AB = $\sqrt{2}$,由正方形AGEF的边长AG = 1,可得AE = $\sqrt{2}$,
∴AB = AE,
∴∠ABE = ∠AEB = $\frac{180° - (90° + 45°)}{2}$ = 22.5°. 如图②,当正方形AGEF在正方形ABCD内部时,AB = AE = $\sqrt{2}$,
∴∠AEB = ∠ABE = $\frac{180° - 45°}{2}$ = 67.5°. 易错提醒:当题目需要通过观察图形来解答时,而题目本身又没有画出图形,这就意味有多种结果,要注意分类讨论.
∴AB = AE,
∴∠ABE = ∠AEB = $\frac{180° - (90° + 45°)}{2}$ = 22.5°. 如图②,当正方形AGEF在正方形ABCD内部时,AB = AE = $\sqrt{2}$,
∴∠AEB = ∠ABE = $\frac{180° - 45°}{2}$ = 67.5°. 易错提醒:当题目需要通过观察图形来解答时,而题目本身又没有画出图形,这就意味有多种结果,要注意分类讨论.
11 (2022·无锡)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG = ________.


答案:
1 解析:连接AG,EG,如图,
∵HG垂直平分AE,
∴AG = EG,
∵正方形ABCD的边长为8,
∴∠B = ∠C = 90°,AB = BC = CD = 8,
∵点E是CD的中点,
∴CE = 4, 设BG = $x$,则CG = 8 - $x$, 由勾股定理,得 EG² = CG² + CE² = (8 - $x$)² + 4²,AG² = AB² + BG² = 8² + $x²$,
∴(8 - $x$)² + 4² = 8² + $x²$, 解得$x$ = 1, 故答案为1.
∵HG垂直平分AE,
∴AG = EG,
∵正方形ABCD的边长为8,
∴∠B = ∠C = 90°,AB = BC = CD = 8,
∵点E是CD的中点,
∴CE = 4, 设BG = $x$,则CG = 8 - $x$, 由勾股定理,得 EG² = CG² + CE² = (8 - $x$)² + 4²,AG² = AB² + BG² = 8² + $x²$,
∴(8 - $x$)² + 4² = 8² + $x²$, 解得$x$ = 1, 故答案为1.
12 (经典题)将边长为2的正方形OABC如图摆放,若∠α = 15°,则点B的坐标为______.


答案:
(-$\sqrt{2}$,$\sqrt{6}$) 解析:作BE⊥x轴于点E.
∵$\alpha$ = 15°,∠AOB = 45°,
∴∠BOE = 60°,
∴∠OBE = 30°.
∵OC = 2,
∴OB = 2$\sqrt{2}$,
∴OE = $\frac{1}{2}$OB = $\sqrt{2}$,由勾股定理得BE = $\sqrt{6}$,
∴点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).
∵$\alpha$ = 15°,∠AOB = 45°,
∴∠BOE = 60°,
∴∠OBE = 30°.
∵OC = 2,
∴OB = 2$\sqrt{2}$,
∴OE = $\frac{1}{2}$OB = $\sqrt{2}$,由勾股定理得BE = $\sqrt{6}$,
∴点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).
13 如图,正方形ABCD的边长为1 cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是________ cm².


答案:
$\frac{2}{3}$
14 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE翻折至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG.
(2)求BG的长.

(1)求证:△ABG≌△AFG.
(2)求BG的长.

答案:
(1)证明:
∵四边形ABCD是正方形,
∴∠B = ∠D = 90°,AD = AB,由折叠的性质可知AD = AF,∠AFE = ∠D = 90°,
∴∠AFG = 90°,AB = AF, 在Rt△ABG和Rt△AFG中,$\begin{cases}AB = AF \\ AG = AG\end{cases}$,
∴Rt△ABG≌Rt△AFG.
(2)解:
∵△ABG≌△AFG,
∴BG = FG, 设BG = FG = $x$,则GC = 6 - $x$.
∵E为CD的中点,
∴CE = EF = DE = 3,
∴EG = $x$ + 3. 在Rt△ECG中,由勾股定理,得CE² + GC² = EG², 即3² + (6 - $x$)² = ($x$ + 3)²,解得$x$ = 2,
∴BG = 2.
(1)证明:
∵四边形ABCD是正方形,
∴∠B = ∠D = 90°,AD = AB,由折叠的性质可知AD = AF,∠AFE = ∠D = 90°,
∴∠AFG = 90°,AB = AF, 在Rt△ABG和Rt△AFG中,$\begin{cases}AB = AF \\ AG = AG\end{cases}$,
∴Rt△ABG≌Rt△AFG.
(2)解:
∵△ABG≌△AFG,
∴BG = FG, 设BG = FG = $x$,则GC = 6 - $x$.
∵E为CD的中点,
∴CE = EF = DE = 3,
∴EG = $x$ + 3. 在Rt△ECG中,由勾股定理,得CE² + GC² = EG², 即3² + (6 - $x$)² = ($x$ + 3)²,解得$x$ = 2,
∴BG = 2.
15 如图①,四边形ABCD是正方形,F是BC边上一点,E是CD边的中点,且AE平分∠DAF.
(1)求证:AF = AD + CF.
(2)AF = DE + BF是否成立,若成立.请给出证明;若不成立,请说明理由.
(3)若四边形ABCD是矩形,其他条件不变,如图②,那么(1)、(2)中的结论是否成立?请你分别作出判断,不要求证明.

(1)求证:AF = AD + CF.
(2)AF = DE + BF是否成立,若成立.请给出证明;若不成立,请说明理由.
(3)若四边形ABCD是矩形,其他条件不变,如图②,那么(1)、(2)中的结论是否成立?请你分别作出判断,不要求证明.

答案:
(1)证明:延长AE交BC的延长线于点G.
∵AE平分∠DAF,
∴∠1 = ∠2.
∵四边形ABCD为正方形.
∴AD//BC,
∴∠1 = ∠G,
∴∠2 = ∠G,
∴AF = GF.
∵E为CD中点,
∴DE = CE. 又
∵∠1 = ∠G,∠AED = ∠GEC,
∴△ADE≌△GCE,
∴AD = CG,
∴AF = GF = CF + CG = AD + CF.
(2)解:成立. 证明:延长CB到点G,使BG = DE,连接AG.
∵四边形ABCD为正方形,
∴AB = AD,∠ADE = 90°,∠ABC = 90°,
∴∠ABG = 90°,
∴∠ABG = ∠ADE. 又
∵BG = DE,
∴△ABG≌△ADE,
∴∠G = ∠AED,∠3 = ∠1.
∵AB//CD,
∴∠BAE = ∠AED,
∴∠4 + ∠2 = ∠AED.
∵AE平分∠DAF,
∴∠1 = ∠2,
∴∠3 = ∠2,
∴∠3 + ∠4 = ∠AED,即∠FAG = ∠AED,
∴∠FAG = ∠G,
∴AF = GF = BG + BF = DE + BF.
(3)
(1)中结论成立,
(2)中结论不成立.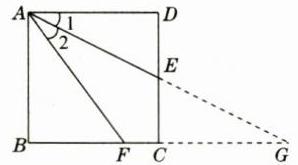

(1)证明:延长AE交BC的延长线于点G.
∵AE平分∠DAF,
∴∠1 = ∠2.
∵四边形ABCD为正方形.
∴AD//BC,
∴∠1 = ∠G,
∴∠2 = ∠G,
∴AF = GF.
∵E为CD中点,
∴DE = CE. 又
∵∠1 = ∠G,∠AED = ∠GEC,
∴△ADE≌△GCE,
∴AD = CG,
∴AF = GF = CF + CG = AD + CF.
(2)解:成立. 证明:延长CB到点G,使BG = DE,连接AG.
∵四边形ABCD为正方形,
∴AB = AD,∠ADE = 90°,∠ABC = 90°,
∴∠ABG = 90°,
∴∠ABG = ∠ADE. 又
∵BG = DE,
∴△ABG≌△ADE,
∴∠G = ∠AED,∠3 = ∠1.
∵AB//CD,
∴∠BAE = ∠AED,
∴∠4 + ∠2 = ∠AED.
∵AE平分∠DAF,
∴∠1 = ∠2,
∴∠3 = ∠2,
∴∠3 + ∠4 = ∠AED,即∠FAG = ∠AED,
∴∠FAG = ∠G,
∴AF = GF = BG + BF = DE + BF.
(3)
(1)中结论成立,
(2)中结论不成立.


查看更多完整答案,请扫码查看


