《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

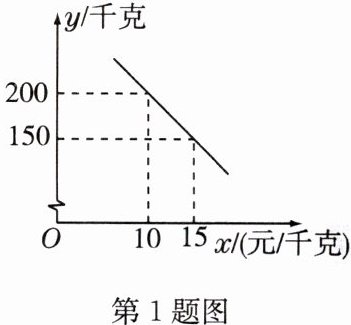
1 某农户承包荒山种植猕猴桃. 到了收获季节，已知猕猴桃销售量$y$(千克)与销售单价$x$(元/千克)之间的函数关系如图所示，则$y$与$x$的函数关系式为（ ）

A. $y=-10x - 300$
B. $y = 10x + 300$
C. $y=-10x + 300$
D. $y = 10x - 300$

答案： C 解析：设y与x的函数关系式为y = kx + b(k ≠ 0)。将点(10,200)，(15,150)分别代入y = kx + b(k ≠ 0)，得 \[ \begin{cases} 10k + b = 200 \\ 15k + b = 150 \end{cases} \] 解得 \[ \begin{cases} k = -10 \\ b = 300 \end{cases} \] 所以y与x的函数关系式为y = -10x + 300。

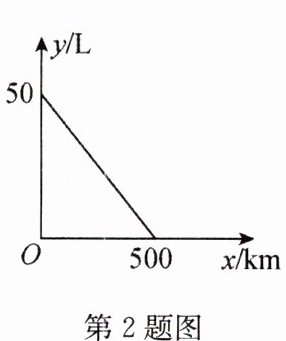
2（2022·哈尔滨）一辆汽车油箱中剩余的油量$y$(L)与已行驶的路程$x$(km)的对应关系如图所示，如果这辆汽车每千米的耗油量相同，那么当油箱中剩余的油量为35 L时，该汽车已行驶的路程为（ ）

A. 150 km
B. 165 km
C. 125 km
D. 350 km

答案： A 解析：设函数解析式为y = kx + b，将(0,50)、(500,0)代入，得 \[ \begin{cases} b = 50 \\ 500k + b = 0 \end{cases} \] 解得 \[ \begin{cases} b = 50 \\ k = -\frac{1}{10} \end{cases} \]
∴函数解析式为y = -\frac{1}{10}x + 50。 当y = 35时，代入解析式得x = 150。故选A。

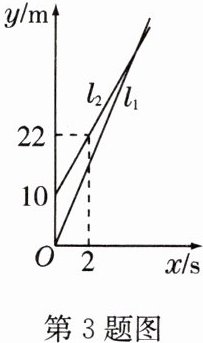
3 甲、乙两人进行比赛，甲比乙跑得快，现在甲让乙先跑10 m，甲再起跑，上图中$l_1$和$l_2$分别表示甲、乙两人跑步的路程$y$(m)与甲跑步的时间$x$(s)之间的函数关系，其中$l_1$的关系式为$y_1 = 8x$，则甲追上乙用了_______s.

答案： 5 解析：设l₂的关系式为y₂ = kx + b(k ≠ 0)。将(0,10)，(2,22)分别代入，得 \[ \begin{cases} 2k + b = 22 \\ b = 10 \end{cases} \] 解得 \[ \begin{cases} k = 6 \\ b = 10 \end{cases} \] 所以y₂ = 6x + 10。 当y₁ = y₂时，8x = 6x + 10，解得x = 5。故甲追上乙用了5 s。

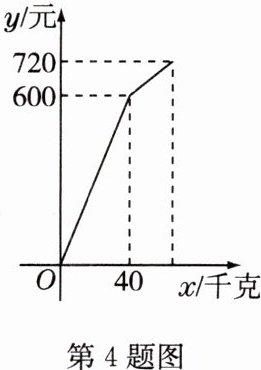
4 小卖部从批发市场购进一批杨梅，在销售了部分杨梅之后，余下的每千克降价3元，直至全部售完. 杨梅销售金额$y$(元)与销售量$x$(千克)之间的关系如图所示. 若销售这批杨梅一共赢利220元，则这批杨梅的进价是（ ）

A. 10元/千克
B. 12元/千克
C. 12.5元/千克
D. 14.4元/千克

答案： A 解析：由图象可知，销售40千克前的售价为600÷40 = 15(元/千克)；40千克后，余下的每千克降价3元，可得此时的售价为15 - 3 = 12(元/千克)，余下的杨梅有(720 - 600)÷12 = 10(千克)。 设进价为t元/千克，则40(15 - t) + 10(12 - t) = 220，解得t = 10。

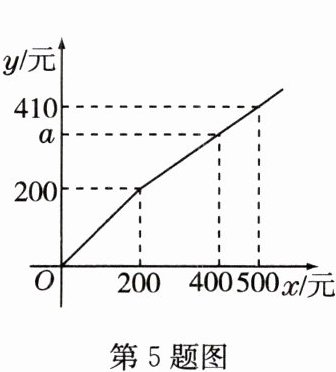
5 某商店在节日期间开展优惠促销活动：凡购买原价超过200元的商品，超过200元的部分可以享受打折优惠. 若购买商品的实际付款金额$y$(单位：元)与商品原价$x$(单位：元)之间的函数关系如图所示，则图中$a$的值是（ ）

A. 300
B. 320
C. 340
D. 360

答案： C 解析：设超过200元部分的y与x的函数关系式为y = kx + b(k ≠ 0，x ＞ 200)，
∵图象过点(200,200)和(500,410)，
∴ \[ \begin{cases} 200k + b = 200 \\ 500k + b = 410 \end{cases} \] 解得 \[ \begin{cases} k = 0.7 \\ b = 60 \end{cases} \]
∴y = 0.7x + 60(x ＞ 200)。 当x = 400时，y = 340，故题图中a的值为340。

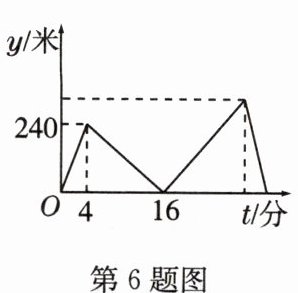
6 小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息. 已知小莹先出发4分钟，在整个步行过程中，两人的距离$y$(米)与小莹出发的时间$t$(分)之间的关系如图所示. 有下列结论：①小莹步行的速度为60米/分；②小亮用16分钟追上小莹；③小亮走完全程用了30分钟；④小亮到达终点时，小莹离终点还有300米. 其中正确的结论有（ ）

A. 1个
B. 2个
C. 3个
D. 4个

答案： B 解析：由题图可得，小莹步行的速度为240÷4 = 60(米/分)，故①正确； 小亮追上小莹用的时间为16 - 4 = 12(分)，故②错误； 小亮走完全程用的时间为2400÷(16×60÷12) = 30(分)，故③正确； 小亮到达终点时，小莹离终点的距离是2400 - (4 + 30)×60 = 360(米)，故④错误。故选B。