《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 如图，在△ABC中，M，N分别为AB，AC的中点，若∠A + ∠B = 130°，∠ANM的度数为（ ）

A. 30°
B. 40°
C. 50°
D. 60°

答案： C

2（2022·常州）如图，在△ABC中，D，E分别是AB，AC边的中点，若DE = 2，则BC的长度是（ ）

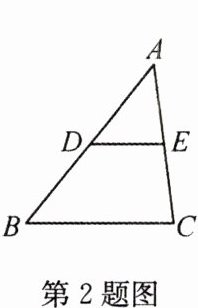
A. 6
B. 5
C. 4
D. 3

答案： C

3 如图，在△ABC中，AB = 8，BC = 6，D，E分别为AC，BC的中点，BF平分∠ABC，交DE于点F，则DF的长为（ ）

A. 1
B. 2
C. 3
D. 4

答案： A

4（2022·丽水）如图，在△ABC中，D，E，F分别是BC，AC，AB的中点.若AB = 6，BC = 8，则四边形BDEF的周长是（ ）

A. 28
B. 14
C. 10
D. 7

答案： B 解析：因为D，E，F分别是BC，AC，AB的中点，所以EF，ED都是△ABC的中位线。所以EF//BC，ED//AB且$EF = \frac{1}{2}BC = \frac{1}{2}×8 = 4$，$ED = \frac{1}{2}AB = \frac{1}{2}×6 = 3$。所以四边形BDEF是平行四边形，所以BD = EF = 4，BF = ED = 3，所以四边形BDEF的周长为BF + BD + ED + EF = 3 + 4 + 3 + 4 = 14。故选B。

5（经典题）如图，在四边形ABCD中，AB = CD，M，N，P分别是AD，BC，BD的中点，若∠ABD = 20°，∠BDC = 70°，则∠PMN = ______°.

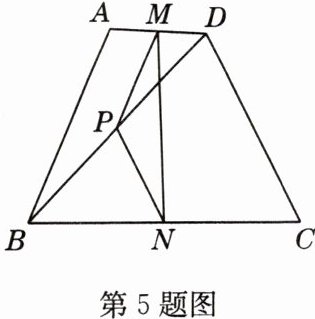
答案： 25 解析：由PM是△ABD的中位线可得PM//AB，$PM = \frac{1}{2}AB$。所以∠MPD = ∠ABD = 20°，由PN为△BCD的中位线可得PN//CD，$PN = \frac{1}{2}CD$，所以∠BPN = ∠BDC = 70°，所以∠NPD = 180° - 70° = 110°。又AB = CD，所以PM = PN，所以∠PMN = ∠PNM = $\frac{180° - (110° + 20°)}{2}=25°$。

6 如图，□ABCD的对角线AC，BD交于点O，点E在AB的延长线上，BF垂直平分CE，垂足为F.如果OF = 4，那么□ABCD的周长是______.

答案： 16 解析：因为四边形ABCD是平行四边形，所以AO = CO。因为BF垂直平分CE，所以CF = EF，所以OF是△ACE的中位线，所以AE = 2OF = 2×4 = 8。又BC = BE，所以AB + BC = 8，所以□ABCD的周长为2×8 = 16。

7 如图，四边形ABCD是平行四边形，点E在对角线AC上，连接BE并延长至点F，使EF = BE，连接DF.求证：DF//AC.

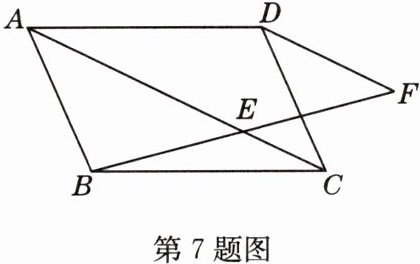
答案： 证明：连接BD交AC于点O。因为四边形ABCD为平行四边形，所以BO = DO。又BE = FE，所以OE是△BDF的中位线，所以OE//DF，所以DF//AC。 名师点睛：平行四边形和中位线“形影不离”，在利用中位线解决问题时，有时要借助平行四边形对角线的交点作为中点来构造中位线。

8（经典题）如图，在四边形ABCD中，∠A = 90°，AB = $3\sqrt{3}$，AD = 3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（ ）

A. 3
B. 4
C. 4.5
D. 5

答案： A 解析：如图，连接DN，DB。因为DE = EM，FN = FM，所以EF是△DNM的中位线，所以$EF = \frac{1}{2}DN$。当点N与点B重合时，DN的值最大，所以EF的值也最大。在Rt△ABD中，因为∠A = 90°，AD = 3，AB = $3\sqrt{3}$，所以$BD = \sqrt{AD^{2}+AB^{2}}=\sqrt{3^{2}+(3\sqrt{3})^{2}} = 6$，所以EF的最大值为$\frac{1}{2}BD = 3$。故选A。