《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

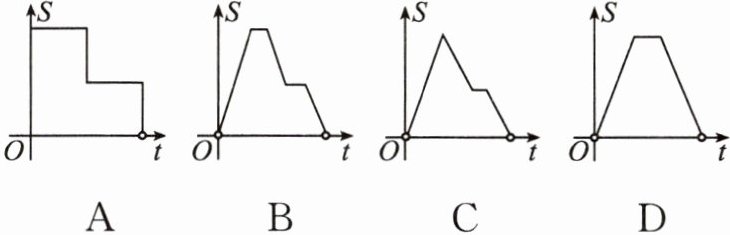
10 (经典题)如图，在边长为2的正方形$ABCD$中剪去一个边长为1的小正方形$CEFG$，动点$P$从点$A$出发，沿$A→D→E→F→G→B$的路线绕多边形的边匀速运动到点$B$时停止(不含点$A$和点$B$)，则$\triangle ABP$的面积$S$随着时间$t$变化的大致的函数图象为（ ）

答案： B 解析：点P在AD上运动时，△ABP的面积S随着时间t的增大而增大；点P在DE上运动时，△ABP的面积S随着时间t的增大保持不变；点P在EF上运动时，△ABP的面积S随着时间t的增大而减小；点P在FG上运动时，△ABP的面积S随着时间t的增大保持不变；点P在GB上运动时，△ABP的面积S随着时间t的增大而减小. 符合要求的只有选项B。

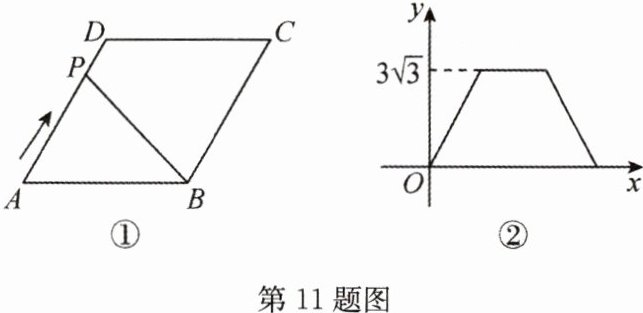
11 (2022·武威)如图①，在菱形$ABCD$中，$\angle A = 60^{\circ}$，动点$P$从点$A$出发，沿折线$AD→DC→CB$方向匀速运动，运动到点$B$停止.设点$P$的运动路程为$x$，$\triangle APB$的面积为$y$，$y$关于$x$的函数图象如图②所示，则$AB$的长为（ ）

A.$\sqrt{3}$
B.$2\sqrt{3}$
C.$3\sqrt{3}$
D.$4\sqrt{3}$

答案： B 解析：如图，连接BD，在菱形ABCD中，∠A = 60°，
∴△ABD为等边三角形， 设AB = a，由题图②可知，△ABD的面积为3√3，
∴√3/4 a² = 3√3。 解得a = 2√3. 故选B。

12 (2022·苏州)有一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完.在整个过程中，容器中的水量$y$(升)与时间$x$(分)之间的函数关系如图所示，则图中$a$的值为_______.

答案： 29/3 解析：依题意，3分钟进水30升，则进水速度为30÷3 = 10(升/分)，
∵3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完， 则排水速度为(8×10－20)÷(8－3) = 12(升/分)，
∴a－8 = 20÷12，解得a = 29/3。 故答案为29/3。

13 (探究题)$A、B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙于同日下午骑摩托车按同样路线从A地出发驶往B地，如图所示，图中的折线PQR和线段MN分别表示甲、乙所行驶的路程$s$(千米)和时间$t$(时)的关系.
根据图象解答下列问题.
(1)甲和乙哪一个出发的更早？早出发多长时间？
(2)甲和乙哪一个早到达B地？早多长时间？
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少？
(4)请你根据图象上的数据，求出乙出发用多长时间就追上甲.

答案： 解：
(1)甲下午1时出发，乙下午2时出发， 所以甲出发更早，早出发1小时。
(2)甲5时到达，乙3时到达， 所以乙更早到达B地，早到2小时。
(3)乙的速度 = 50÷(3－2) = 50(千米/时)， 甲的平均速度 = 50÷(5－1) = 12.5(千米/时)。
(4)设乙出发x小时就追上甲. 根据题意，得50x = 20 + 10x， 解得x = 0.5。 答：乙出发0.5小时就追上甲。