《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

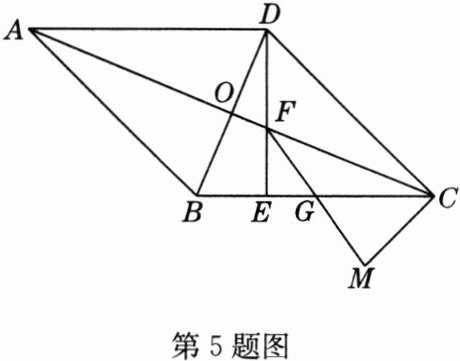
5 如图，已知菱形ABCD的对角线相交于点O，∠BAD = 45°，DE⊥BC于点E，交AC于点F，点G是BC的中点，连接FG，过点C作CM⊥CD交FG的延长线于点M.
求证：CM + 2EF = BC.

答案： 证明：连接BF，如图所示，因为四边形ABCD是菱形，所以∠BAF = ∠DAF，AB = AD = BC = CD，AD//BC，AB//CD。因为DE⊥BC，所以DE⊥AD，所以∠ADF = 90°，在△ABF和△ADF中，AB = AD，∠BAF = ∠DAF，AF = AF，所以△ABF≌△ADF(SAS)，所以∠ABF = ∠ADF = 90°，BF = DF，所以BF⊥AB。因为CM⊥CD，所以BF//CM，所以∠GFB = ∠M。因为点G是BC的中点，所以BG = CG。在△BFG和△CMG中，∠BFG = ∠M，∠BGF = ∠CGM，BG = CG，所以△BFG≌△CMG(AAS)，所以BF = CM，所以CM = BF = DF，因为BF//CM，∠BCD = ∠BAD = 45°，CM⊥CD，所以∠GBF = ∠GCM = 90° - 45° = 45°，所以△BEF和△DEC是等腰直角三角形，所以BE = EF，DE = EC，所以CM + 2EF = DF + EF + BE = DE + BE = BC。

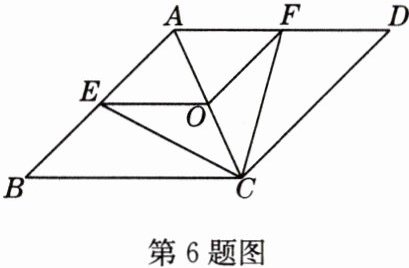
6 已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF.
(1)求证：△BCE≌△DCF.
(2)当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由.

答案： （1）证明：因为四边形ABCD是菱形，所以∠B = ∠D，AB = BC = DC = AD，因为点E，O，F分别为AB，AC，AD的中点，所以AE = BE = DF = AF，OF = $\frac{1}{2}$DC，OE = $\frac{1}{2}$BC，在△BCE和△DCF中，BE = DF，∠B = ∠D，BC = DC，所以△BCE≌△DCF(SAS)。 （2）解：当AB⊥BC时，四边形AEOF是正方形。理由如下：由（1）得AE = OE = OF = AF，所以四边形AEOF是菱形。因为AB⊥BC，OE//BC，所以OE⊥AB，所以∠AEO = 90°，所以四边形AEOF是正方形。

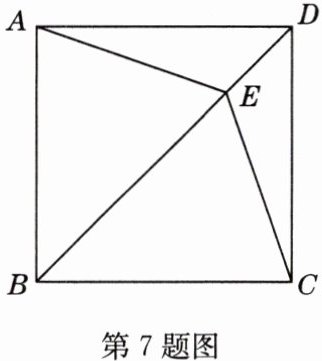
7 已知：如图，四边形ABCD中，AD//BC，AD = CD，E是对角线BD上一点，且EA = EC.
(1)求证：四边形ABCD是菱形.
(2)如果BE = BC，且∠CBE∶∠BCE = 2∶3，求证：四边形ABCD是正方形.

答案： 证明：（1）在△ADE与△CDE中，AD = CD，DE = DE，EA = EC，所以△ADE≌△CDE，所以∠ADE = ∠CDE。因为AD//BC，所以∠ADE = ∠CBD，所以∠CDE = ∠CBD，所以BC = CD。因为AD = CD，所以BC = AD。又AD//BC，所以四边形ABCD为平行四边形，因为AD = CD，所以平行四边形ABCD是菱形。 （2）因为BE = BC，所以∠BCE = ∠BEC。因为∠CBE : ∠BCE = 2 : 3，所以∠CBE = 180×$\frac{2}{2 + 3 + 3}$ = 45°。因为四边形ABCD是菱形，所以∠ABE = 45°，所以∠ABC = 90°，所以菱形ABCD是正方形。

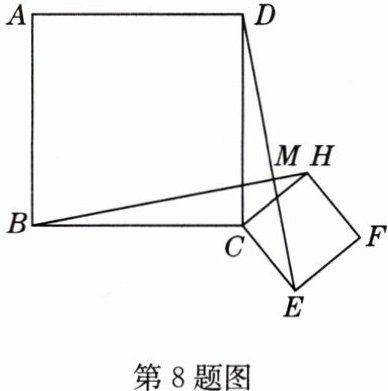
8 在平面内，正方形ABCD与正方形CEFH如图放置，连接DE，BH，两线交于点M.
求证：(1)BH = DE；(2)BH⊥DE.

答案： 证明：（1）在正方形ABCD与正方形CEFH中，BC = DC，CE = CH，∠BCD = ∠ECH = 90°，所以∠BCD + ∠DCH = ∠ECH + ∠DCH，即∠BCH = ∠DCE，在△BCH和△DCE中，BC = DC，∠BCH = ∠DCE，CH = CE，所以△BCH≌△DCE(SAS)，所以BH = DE。 （2）设BH与CD交于点G。因为△BCH≌△DCE，所以∠CBH = ∠CDE。又因为∠CGB = ∠MGD，∠CGB + ∠CBG = 90°，所以∠DGM + ∠GDM = 90°，所以∠DMB = 90°，所以BH⊥DE。