《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 如图，□ABCD中，AB = 2，AD = 4，对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点，则下列说法正确的是 （ ）

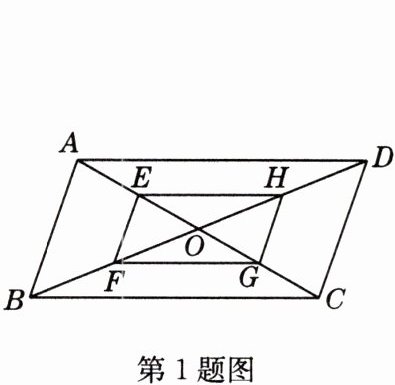
A. EH = HG
B. 四边形EFGH是平行四边形
C. AC⊥BD
D. △ABO的面积是△EFO面积的2倍

答案： B - **解析**：因为E，F，G，H分别是AO，BO，CO，DO的中点，在□ABCD中，AB = 2，AD = 4，所以EH = $\frac{1}{2}$AD = 2，HG = $\frac{1}{2}$CD = $\frac{1}{2}$AB = 1，所以EH ≠ HG，故选项A错误；因为E，F，G，H分别是AO，BO，CO，DO的中点，所以EH//FG，EH = $\frac{1}{2}$AD = $\frac{1}{2}$BC = FG，所以四边形EFGH是平行四边形，故选项B正确；由题目中的条件，无法判断AC和BD是否垂直，故选项C错误；连接AF，因为点E，F分别为OA和OB的中点，所以$S_{\triangle ABO}$ = 2$S_{\triangle AFO}$ = 4$S_{\triangle EFO}$，即△ABO的面积是△EFO的面积的4倍，故选项D错误。

2（经典题）□ABCD中，E，F是对角线BD上不同的两点. 下列条件中，不能得出四边形AECF一定为平行四边形的是 （ ）
A. BE = DF
B. AE = CF
C. AF//CE
D. ∠BAE = ∠DCF

答案： B - **解析**：如图，连接AC，与BD相交于O，在□ABCD中，OA = OC，OB = OD，要使四边形AECF为平行四边形，只需证明得到OE = OF即可。\nA. 若BE = DF，则OB - BE = OD - DF，即OE = OF，故本选项不符合题意；\nB. 根据AE = CF无法判断出OE = OF，故本选项符合题意；\nC. 若AF//CE，能够利用“角角边”证明△AOF和△COE全等，从而得到OE = OF，故本选项不符合题意；\nD. 若∠BAE = ∠DCF，能够利用“角边角”证明△ABE和△CDF全等，从而得到BE = DF，根据A选项的分析过程，可以得到OE = OF，故本选项不符合题意。

3 如图，在Rt△ABC中，∠ACB = 90°，∠A = 30°，D，E，F分别为AB，AD，AC的中点，若CB = 4，则EF的长度为 （ ）

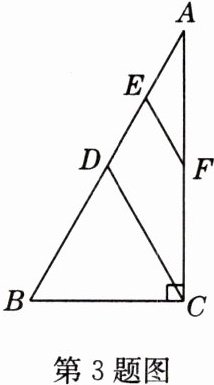
A. 2
B. 1
C. $\frac{3}{2}$
D. $2\sqrt{3}$

答案： A - **解析**：因为∠ACB = 90°，∠A = 30°，所以AB = 2BC = 8。因为∠ACB = 90°，D为AB的中点，所以CD = $\frac{1}{2}$AB = 4。因为E，F分别为AD，AC的中点，所以EF = $\frac{1}{2}$CD = 2。

4 如图，分别以Rt△ABC的直角边AC及斜边AB为边作等边△ACD及等边△ABE，已知∠BAC = 30°，EF⊥AB，垂足为F，连接DF交AC于点O. 有下列说法：①AC = EF；②四边形ADFE是平行四边形；③△ABC≌△ADO；④BC = 2FO；⑤∠EAD = 120°. 其中正确结论的个数是 （ ）

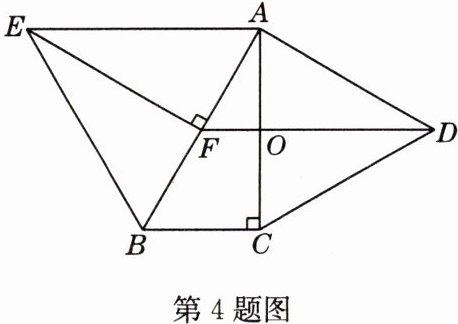
A. 2
B. 3
C. 4
D. 5

答案： B - **解析**：因为Rt△ABC中，∠BAC = 30°，所以AB = 2BC。又因为△ABE是等边三角形，EF⊥AB，所以AB = 2AF，所以AF = BC。在Rt△AFE和Rt△BCA中，$\begin{cases}AF = BC\\AE = BA\end{cases}$，所以Rt△AFE≌Rt△BCA(HL)，所以AC = EF，故①正确。因为△ACD是等边三角形，所以∠DAC = 60°，AC = AD，所以∠DAB = ∠DAC + ∠BAC = 90°。又因为EF⊥AB，所以EF//AD。因为AC = EF，AC = AD，所以EF = AD，所以四边形ADFE是平行四边形，故②正确。因为四边形ADFE是平行四边形，所以AE = DF = AB，AE//DF。又因为AF = BC，AD = AC，所以△ADF≌△CAB(SSS)，所以△ABC与△ADO不全等，故③错误。因为AE//DF，所以$\frac{AF}{BA}$ = $\frac{FO}{BC}$ = $\frac{1}{2}$，所以BC = 2FO，故④正确。因为∠EAD = ∠BAE + ∠BAC + ∠CAD = 150°，故⑤错误。

5 如图，在△ABC中，∠C = 90°，E是CA延长线上一点，F是CB上一点，AE = 12，BF = 8，点P，Q，D分别是AF，BE，AB的中点，则PQ的长为 （ ）

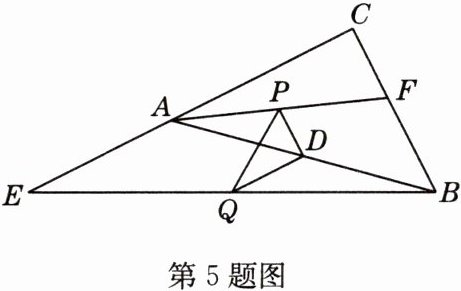
A. $2\sqrt{13}$
B. 4
C. 6
D. $3\sqrt{5}$

答案： A - **解析**：因为∠C = 90°，所以∠CAB + ∠CBA = 90°，因为点P，D分别是AF，AB的中点，所以PD = $\frac{1}{2}$BF = 4，PD//BF，所以∠ADP = ∠ABC。同理，DQ = $\frac{1}{2}$AE = 6，∠ADQ = ∠CAB，所以∠PDQ = ∠ADP + ∠ADQ = 90°，由勾股定理得PQ = $\sqrt{PD^{2}+DQ^{2}}$ = 2$\sqrt{13}$。

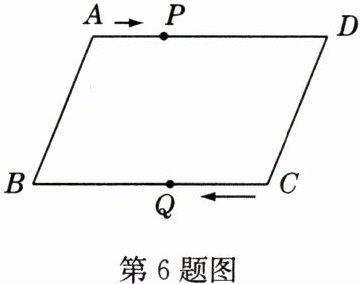
6（易错题）如图，在平行四边形ABCD中，AB = 8 cm，AD = 12 cm，点P在AD边上，以每秒1 cm的速度从点A向点D运动，点Q在BC边上，以每秒4 cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动开始后，以P、D、Q、B四点为顶点组成平行四边形的次数有________次.

答案： 3 - **解析**：设经过t秒，以点P、D、Q、B为顶点的四边形组成平行四边形，因为以点P、D、Q、B为顶点组成平行四边形，所以DP = BQ，分为以下情况：\n①点Q的运动路线是C - B，方程为12 - 4t = 12 - t，此时解得t = 0，不符合题意；\n②点Q的运动路线是C - B - C，方程为4t - 12 = 12 - t，解得t = 4.8；\n③点Q的运动路线是C - B - C - B，方程为12 - (4t - 24) = 12 - t，解得t = 8；\n④点Q的运动路线是C - B - C - B - C，方程为4t - 36 = 12 - t，解得t = 9.6；\n⑤点Q的运动路线是C - B - C - B - C - B，方程为12 - (4t - 48) = 12 - t，解得t = 16，此时P点走的路程为16＞AD，此时不符合题意。所以共3次。故答案为3。 - **注意**：此题考查了平行四边形的判定。能求出符合条件的所有情况是解此题的关键，注意分类讨论思想的应用。

7（易错题）在△ABC中，AB = AC，点D在边BC所在的直线上，过点D作DF//AC交直线AB于点F，DE//AB交直线AC于点E. 若AC = 7，DE = 5，则DF =________.

答案： 2或12 - **解析**：如图①，当点D在线段BC上时，因为DE//AB，DF//AC，所以四边形AEDF是平行四边形，所以AF = DE = 5。因为AB = AC = 7，所以BF = 7 - 5 = 2，∠B = ∠C。因为DF//AC，所以∠FDB = ∠C，所以∠B = ∠FDB，所以DF = BF = 2。如图②，当点D在BC的延长线上时，同法可证，DE = AF = 5，FB = FD，因为AB = AC = 7，所以DF = FB = 5 + 7 = 12。综上所述，DF的值为2或12。