《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

8（2022·重庆A卷，中）若一个四位数M的个位数字与十位数字的平方和恰好是M去掉个位与十位数字后得到的两位数，则这个四位数M为“勾股和数”.
例如：M = 2543，∵3² + 4² = 25，∴2543是“勾股和数”；
又如：M = 4325，∵5² + 2² = 29，29 ≠ 43，∴4325不是“勾股和数”.
(1)判断2022，5055是否是“勾股和数”，并说明理由；
(2)一个“勾股和数”M的千位数字为a，百位数字为b，十位数字为c，个位数字为d，记G(M) = $\frac{c + d}{9}$，P(M) = $\frac{|10(a - c)+(b - d)|}{3}$.当G(M)，P(M)均是整数时，求出所有满足条件的M.

答案： 解：
(1)$2022$不是“勾股和数”，$5055$是“勾股和数”。 理由：$\because2^{2}+2^{2}=8,8\neq20$， $\therefore2022$不是“勾股和数”； $\because5^{2}+5^{2}=50,50 = 50$， $\therefore5055$是“勾股和数”。
(2)$\because M$为“勾股和数”， $\therefore10a + b=c^{2}+d^{2}$， $\therefore0\lt c^{2}+d^{2}\lt100$， $\because G(M)=\frac{c + d}{9}$为整数， $\therefore c + d = 9$， $\because P(M)=\frac{|10(a - c)+(b - d)|}{3}=\frac{|10a + b-10c - d|}{3}=\frac{|c^{2}+d^{2}-9c - 9|}{3}$为整数， $\therefore c^{2}+d^{2}=81 - 2cd$为$3$的倍数， $\therefore$①$c = 0,d = 9$或$c = 9,d = 0$，此时$M = 8109$或$8190$； ②$c = 3,d = 6$或$c = 6,d = 3$，此时$M = 4536$或$4563$。 综上，$M$的值为$8109$或$8190$或$4536$或$4563$。

9（2022·十堰，难）【阅读材料】如图①，四边形ABCD中，AB = AD，∠B + ∠D = 180°，点E，F分别在BC，CD上，若∠BAD = 2∠EAF，则EF = BE + DF.

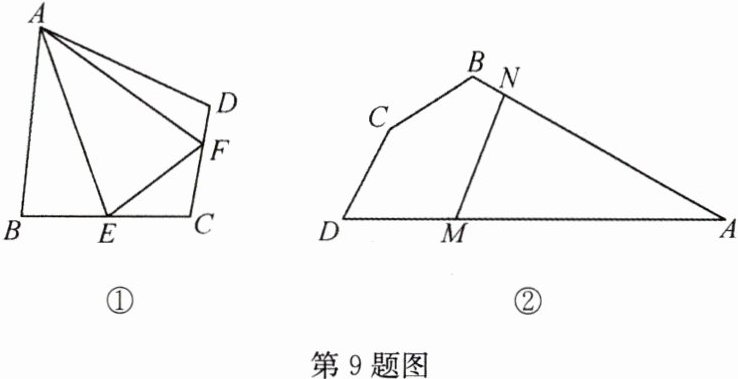
【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD.已知CD = CB = 100 m，∠D = 60°，∠ABC = 120°，∠BCD = 150°，道路AD，AB上分别有景点M，N，且DM = 100 m，BN = 50($\sqrt{3}$ - 1)m，若在M，N之间修一条直路，则路线M→N的长比路线M→A→N的长少________ m(结果取整数,参考数据:$\sqrt{3}$≈1.7).

答案：
$370$ 解析：如图，延长$AB,DC$交于点$E$，连接$CM,CN,BM$，

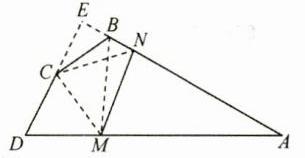
$\because\angle D = 60^{\circ},\angle ABC = 120^{\circ},\angle BCD = 150^{\circ}$， $\therefore\angle A = 30^{\circ},\angle E = 90^{\circ}$， $\because DC = DM = 100,\therefore\triangle DCM$是等边三角形， $\therefore\angle DCM = 60^{\circ},\therefore\angle BCM = 90^{\circ}$， 在$Rt\triangle BCE$中，$BC = 100,\angle ECB = 180^{\circ}-\angle BCD = 30^{\circ}$， $\therefore EB=\frac{1}{2}BC = 50\ m,EC=\sqrt{3}EB = 50\sqrt{3}\ m$， $\therefore DE = DC + EC=(100 + 50\sqrt{3})\ m$， $Rt\triangle ADE$中，$AD = 2DE=(200 + 100\sqrt{3})\ m,AE=\sqrt{3}DE=(100\sqrt{3}+150)\ m$， $\therefore AM = AD - DM = 200 + 100\sqrt{3}-100=(100 + 100\sqrt{3})\ m$， $AN = AB - BN=(AE - EB)-BN=(100\sqrt{3}+150 - 50)-50(\sqrt{3}-1)=(50\sqrt{3}+150)\ m$， $\therefore AM + AN = 100 + 100\sqrt{3}+50\sqrt{3}+150=(250 + 150\sqrt{3})\ m$， $Rt\triangle CMB$中，$BM=\sqrt{BC^{2}+CM^{2}}=100\sqrt{2}\ m$， $\because EN = EB + BN = 50 + 50(\sqrt{3}-1)=50\sqrt{3}=EC$， $\therefore\triangle ECN$是等腰直角三角形。 $\therefore\angle NCM=\angle BCM-\angle NCB=\angle BCM-(\angle NCE-\angle BCE)=75^{\circ}=\frac{1}{2}\angle DCB$。 由阅读材料可得$MN = DM + BN = 100 + 50(\sqrt{3}-1)=50(\sqrt{3}+1)\ m$， $\therefore$路线$M\rightarrow N$的长比路线$M\rightarrow A\rightarrow N$的长少$250 + 150\sqrt{3}-50(\sqrt{3}+1)=200 + 100\sqrt{3}\approx370(m)$。