《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 点A，B，C是平面内不在同一条直线上的三个点，点D是平面内任意一点，若A，B，C，D四点恰好能构成平行四边形，则在平面内符合这样条件的点D有（ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： C

2 如图，□ABCD中，EF//AD，HN//AB，则图中的平行四边形有（ ）


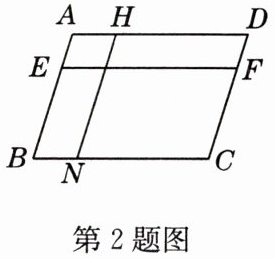
A. 12个
B. 9个
C. 7个
D. 5个

答案： B

3 若□ABCD中，已知∠A - ∠B = 80°，则∠A的度数为（ ）
A. 80°
B. 100°
C. 130°
D. 140°

答案： C

4 如图，在□ABCD中，AB = 3，BC = 5，∠ABC的平分线交AD于点E，则线段DE的长为（ ）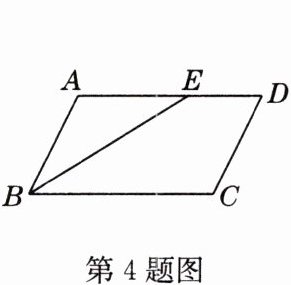
A. 5
B. 4
C. 3
D. 2

答案： D

5（2022·大庆）如图，将平行四边形ABCD沿对角线BD折叠，使点A落在点E处.若∠1 = 56°，∠2 = 42°，则∠A的度数为（ ）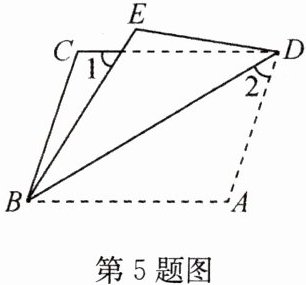
A. 108°
B. 109°
C. 110°
D. 111°

答案： 解析：
∵四边形ABCD为平行四边形，
∴AB//CD，
∴∠ABE = ∠1 = 56°， 根据折叠可知，∠ABD = ∠EBD，
∴∠ABD = $\frac{1}{2}$∠ABE = $\frac{1}{2}$×56° = 28°，
∵∠2 = 42°，
∴∠A = 180° - ∠ABD - ∠2 = 110°，故C正确. 故选C.

6 (经典题)如图，□ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A落在边CD上的点F处.若△DEF的周长为8，△CBF的周长为18，则FC的长为_______.

答案： 解析：由折叠可知EF = EA，由△DEF的周长为8可得AD + DF = 8. 由折叠可知BF = BA，由△CBF的周长为18可得AB + BC + CF = 18.
∴□ABCD的周长为8 + 18 = 26，
∴AD + DC = 13. 又AD + DF = 8，
∴CF = 13 - 8 = 5.

7 已知，在□ABCD中，∠A = 45°，BC = 2，则AB与CD之间的距离为_______.

答案： $\sqrt{2}$ 解析：如图，作DE⊥AB于点E.
∵∠A = 45°，
∴∠ADE = ∠A = 45°，
∴DE = AE.
∵AD = BC = 2，
∴由勾股定理可得DE = $\sqrt{2}$，
∴AB与CD之间的距离为$\sqrt{2}$.

8 已知□ABCD的周长为24 cm，AD与BC之间的距离为3 cm，AB与CD之间的距离为5 cm，则AB、BC的长分别为_______.

答案： $\frac{9}{2}$ cm $\frac{15}{2}$ cm 解析：设BC = x cm，AB = y cm，则 $\begin{cases}x + y = 12 \\ 3x = 5y\end{cases}$，解得$\begin{cases}x = \frac{15}{2} \\ y = \frac{9}{2}\end{cases}$，
∴AB = $\frac{9}{2}$ cm，BC = $\frac{15}{2}$ cm.

9 (易错题)如图，在□ABCD中，∠A = 70°，将□ABCD折叠，使点D，C分别落在直线AB上的点F，E处，折痕为MN，则∠AMF等于（ ）
A. 70°
B. 40°
C. 30°
D. 20°

答案： B 解析：
∵在□ABCD中，AB//CD，
∴∠A + ∠D = 180°，又∠A = 70°，
∴∠D = 110°.
∴∠MFE = ∠D = 110°，
∴∠AMF = 110° - 70° = 40°.