《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 已知矩形的周长为20，相邻两边的长分别为x和y，则y与x的函数解析式为 （ ）
A. $y = x + 10$
B. $y = -x + 10$
C. $y = x + 20$
D. $y = -x + 20$

答案： B

2 等腰三角形的周长为60 cm，底边长为x cm，一腰长为y cm，则y关于x的函数解析式及自变量的取值范围是 （ ）
A. $y = 60 - 2x(0 ＜ x ＜ 60)$
B. $y = 60 - 2x(0 ＜ x ＜ 30)$
C. $y = \frac{1}{2}(60 - x)(0 ＜ x ＜ 60)$
D. $y = \frac{1}{2}(60 - x)(0 ＜ x ＜ 30)$

答案： D 解析：$x + 2y = 60$，$2y = 60 - x$，$y = \frac{1}{2}(60 - x)$。 $\because 2y ＞ x$，即$60 - x ＞ x$，$\therefore x ＜ 30$， 又$x ＞ 0$，$\therefore 0 ＜ x ＜ 30$。

3 多边形的内角和与边数分别用y，x来表示，则y与x的函数解析式为_____________.

答案： $y = 180^{\circ}(x - 2)$

4 已知x是y的算术平方根，则y与x的函数解析式为_____________.

答案： $y = x^{2}(x \geq 0)$

5 在某次实验中，测得两个变量m和v之间的4组对应数据如下表：

则m与v之间的关系接近于下列各关系式中的 （ ）
A. $v = 2m - 2$
B. $v = m^2 - 1$
C. $v = 3m - 3$
D. $v = m + 1$

答案： B

6 星期天，小宇同学骑自行车从家出发到图书馆查阅有关资料，之后就返回了家，如图反映了小宇离家的路程y（米）与骑车时间x（分）的函数关系.从图象得到下列信息，其中错误的是 （ ）

A. 小宇家与图书馆之间的路程是3千米
B. 小宇在图书馆查阅资料用了42分钟
C. 小宇从图书馆骑车回家用了10分钟
D. 小宇从家到图书馆骑车的速度比返回的速度慢

答案： B

7 已知A，B两地相距10千米，上午9：00甲骑电动车从A地出发到B地，9：10乙开车从B地出发到A地，甲、乙两人距A地的距离y（千米）与甲所用的时间x（分）之间的关系如图所示，则乙到达A地的时间为_________.

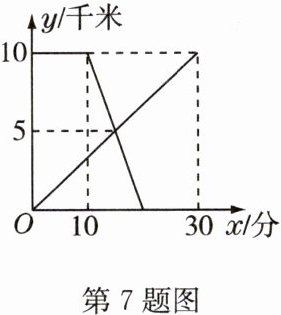
答案： 9:20 解析：因为甲30分钟走完全程10千米，所以甲的速度是$\frac{1}{3}$千米/分，由题图中看出两人在走了5千米时相遇，那么甲此时走了15分钟，则乙走了(15 - 10)分钟，所以乙的速度为5÷5 = 1(千米/分)，所以乙走完全程需要时间为10÷1 = 10(分)，故乙到达A地的时间为9:20。

8 (原创题)如图，在△ABC中，∠ACB = 90°，AC = 6，BC = 8，P是AB边上一动点(不与端点B重合)，点P由点A向点B运动，运动的路程为x，△BCP的面积为y，则y与x的函数关系式为 （ ）

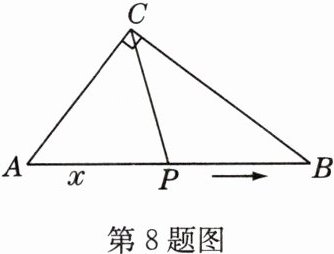
A. $y = \frac{12}{5}(10 - x)$
B. $y = \frac{24}{5}(10 - x)$
C. $y = \frac{12}{5}x$
D. $y = \frac{24}{5}x$

答案： A 解析：如图，作$CD \perp AB$于点D。由勾股定理可得$AB = 10$。易求$CD = \frac{24}{5}$。$\therefore y = S_{\triangle BCP} = \frac{1}{2}PB \cdot CD = \frac{1}{2}(10 - x) \cdot \frac{24}{5} = \frac{12}{5}(10 - x)$。![img id=1]