《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

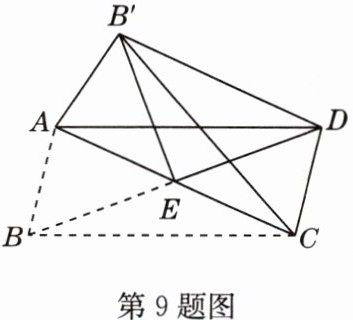
9 如图，□ABCD中，对角线AC、BD相交于点E，∠AEB = 45°，BD = 2，将△ABC沿AC折叠，点B落在点B′处，连接B′E，B′D，则DB′的长为_______.

答案： $\sqrt{2}$ 解析：
∵在□ABCD中，BD = 2，
∴BE = DE = 1，由题意可知∠BEB' = 90°，B'E = DE，
∴∠DEB' = 90°，
∴$DB'^{2}=DE^{2}+B'E^{2}=1^{2}+1^{2}=2$，
∴DB' = $\sqrt{2}$。

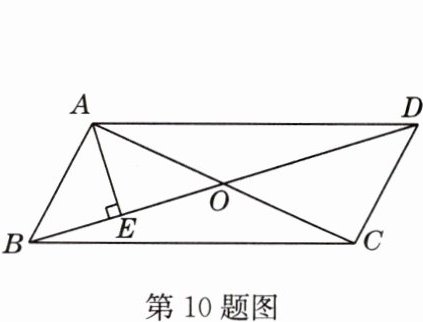
10 如图，在□ABCD中，对角线AC、BD相交于点O，AE⊥BD于点E，∠BAE = 45°，AE = 2 cm，AC + BD = 12 cm，则△COD的周长为_______.

答案： $(6 + 2\sqrt{2})$cm

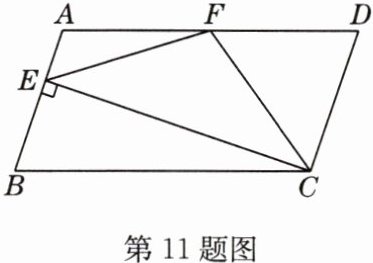
11 如图，在□ABCD中，AD = 2AB，F是AD的中点，作CE⊥AB，垂足为E，连接EF、CF，则下列结论一定正确的是_______.（把所有正确结论的序号都填在横线上）
①∠DCF = $\frac{1}{2}$∠BCD；②EF = CF；③S△BEC = 2S△CEF；④∠DFE = 3∠AEF.

答案： ①②④

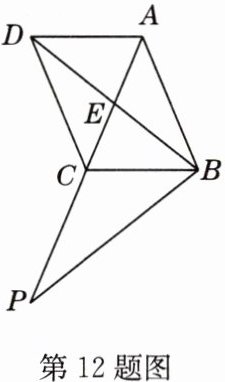
12 如图，□ABCD中，AC = AB，延长AC到点P，使CP = CA，BD交AC于点E. 求证：BP = 2BE.

答案： 证明：
∵AC = AB，
∴∠ABC = ∠ACB。
∵四边形ABCD为平行四边形，
∴DC//AB，
∴∠DCB + ∠ABC = 180°。又
∵∠PCB + ∠ACB = 180°，
∴∠PCB = ∠DCB。又AC = AB = DC，PC = AC，
∴PC = DC。又CB = CB，
∴△PCB≌△DCB，
∴PB = DB。又$BE=\frac{1}{2}DB$，
∴PB = 2BE。

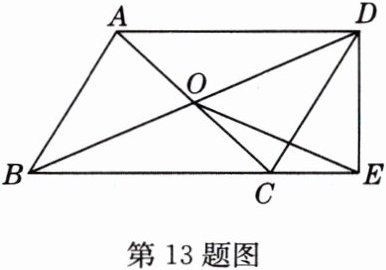
13（创新题）如图，□ABCD的对角线AC、BD相交于点O，E为BC延长线上的一点，且OE = OB，连接DE. 求证：△BDE为直角三角形.

答案： 证明：
∵四边形ABCD为平行四边形，
∴BO = DO。又
∵EO = BO，
∴BO = EO = DO，
∴∠OBE = ∠OEB，∠ODE = ∠OED。
∵∠OBE + ∠OEB + ∠OED + ∠ODE = 180°，
∴∠OEB + ∠OED = 90°，
∴∠BED = 90°，
∴△BDE为直角三角形。

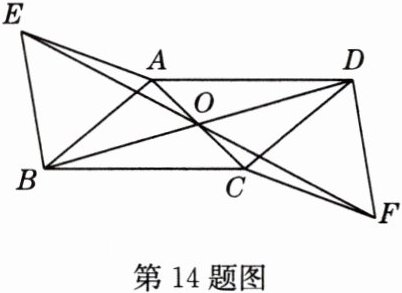
14（原创题）如图，□ABCD的对角线AC、BD相交于点O，分别以AB、CD为边向外作等边△ABE和等边△CDF，连接EO、FO，求证：E、O、F三点在同一条直线上.

答案： 证明：
∵四边形ABCD为平行四边形，
∴AB//CD，AO = CO，
∴∠BAO = ∠DCO。
∵△ABE和△CDF均为等边三角形，
∴AB = AE，CD = CF，∠BAE = ∠DCF = 60°，
∴AE = CF，∠OAE = ∠OCF，
∴△AOE≌△COF，
∴∠AOE = ∠COF。
∵∠AOE + ∠EOC = 180°，
∴∠COF + ∠EOC = 180°，
∴E、O、F三点在同一条直线上。

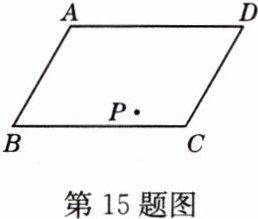
15 如图所示，王老汉家有一块平行四边形的土地，地中有一口井P，王老汉的两个儿子要平分这块地，且使这口井在地界上，你能帮助他们把地分开吗？请画出图形，并说明理由.

答案： 解：连接AC，BD相交于点O，过O，P两点作一条直线分别交AD，BC于点E，F，则直线OP把□ABCD平分。 理由：在□ABCD中，AD//CB，AB = CD，AO = CO，BO = DO，则易证△AEO≌△CFO，△AOB≌△COD，△BOF≌△DOE，
∴$S_{四边形ABFE}=S_{四边形CDEF}$。