《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 (易错题)如图，E为正方形ABCD对角线AC上一点，连接BE，DE，则图中全等三角形有 （ ）

A. 1对
B. 2对
C. 3对
D. 4对

答案： C

2 如图，正方形ABCD的对角线AC，BD相交于点O，作OE⊥OF，分别交AB，BC于点E，F，若AE = 4，CF = 3，则EF等于 （ ）

A. 7
B. 5
C. 4
D. 3

答案： B 解析：易证△BOE≌△COF，
∴BE = CF = 3. 又AB = CB，
∴BF = AE = 4. 又∠EBF = 90°，
∴由勾股定理得EF = 5.

3 (2022·重庆B卷)如图，在正方形ABCD中，对角线AC，BD相交于点O. E，F分别为AC，BD上一点，且OE = OF，连接AF，BE，EF. 若∠AFE = 25°，则∠CBE的度数为 （ ）

A. 50°
B. 55°
C. 65°
D. 70°

答案： C 解析：在正方形ABCD中，AO = BO，∠AOD = ∠AOB = 90°，∠CBO = 45°，
∵OE = OF，
∴△AOF≌△BOE(SAS)，
∴∠OBE = ∠OAF，
∵OE = OF，∠EOF = 90°，
∴∠OEF = ∠OFE = 45°，
∵∠AFE = 25°，
∴∠OAF = ∠OEF - ∠AFE = 20°，
∴∠CBE = ∠CBO + ∠OBE = 45° + 20° = 65°. 故选C.

4 (易错题)在正方形ABCD中，以CD为边，在正方形ABCD外作等边三角形CDE，连接AE，与对角线BD交于点F，连接CF，则∠BFC的度数为________.

答案： 60° 解析：如图，由AD = CD = DE得∠DAE = ∠DEA. 又∠ADE = 90° + 60° = 150°，
∴∠DAE = $\frac{180° - 150°}{2}$ = 15°，易证∠DCF = ∠DAF = 15°，
∴∠BFC = ∠DCF + ∠CDF = 15° + 45° = 60°.

5 如图，菱形ABCD的面积为120 cm²，正方形AECF的面积为50 cm²，则菱形的边长为________.

答案： 13 cm 解析：
∵四边形AECF为正方形，
∴AC = EF. 又
∵$\frac{1}{2}$·AC·EF = 50，
∴AC = 10 cm.
∵四边形ABCD为菱形，
∴$\frac{1}{2}$·AC·BD = 120，
∴BD = 24 cm. 又
∵AO = CO = 5 cm，BO = DO = 12 cm，
∴AB = 13 cm.
∴菱形ABCD的边长为13 cm.

6 已知四边形ABCD是平行四边形，下列结论不正确的是 （ ）
A. 当AB = BC时，它是菱形
B. 当AC⊥BD时，它是菱形
C. 当∠ABC = 90°时，它是矩形
D. 当AC = BD时，它是正方形

答案： D

7 如图，□ABCD是菱形，对角线AC，BD相交于点O，添加一个条件使得四边形ABCD是正方形，这个条件可以是________.

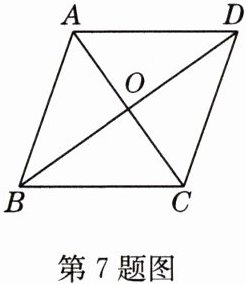
答案： ∠ABC = 90°(答案不唯一)

8 如图，□ABCD中，AC，BD交于点O，E是BD延长线上一点，且△ACE是等边三角形.
(1)求证：四边形ABCD是菱形.
(2)若∠AED = 2∠EAD，求证：四边形ABCD为正方形.

答案： 证明：
(1)
∵四边形ABCD为平行四边形，
∴AO = CO. 又△ACE为等边三角形，
∴EO⊥AC，即DB⊥AC，
∴四边形ABCD为菱形.
(2)设∠EAD = $x^{\circ}$，则∠AED = $2x^{\circ}$，
∴∠ADO = ∠EAD + ∠AED = $x^{\circ}$ + $2x^{\circ}$ = $3x^{\circ}$. ∠DAO = 60° - $x^{\circ}$. 又∠AOD = 90°，
∴∠DAO + ∠ADO = 90°，
∴60 - $x$ + 3$x$ = 90，
∴$x$ = 15，
∴∠DAO = 60° - $x^{\circ}$ = 60° - 15° = 45°，∠ADO = $3x^{\circ}$ = 3×15° = 45°，
∴∠DAO = ∠ADO，
∴AO = DO. 又AO = CO，BO = DO，
∴AC = BD，
∴菱形ABCD是正方形.

9 如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高.有下面四个结论：①OA = OD；②AD⊥EF；③当∠BAC = 90°时，四边形AEDF是正方形；④AE² + DF² = AF² + DE².
其中正确的是 （ ）

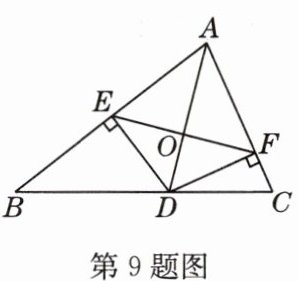
A. ②③
B. ②④
C. ①③④
D. ②③④

答案： D 解析：①不正确；②已知AD平分∠BAC，DE⊥AB，DF⊥AC，根据角平分线上的点到角两边的距离相等，可得DE = DF，又AD = AD，所以Rt△AED≌Rt△AFD，所以AE = AF，又DE = DF，所以AD垂直平分EF，所以②正确；③因为∠BAC = ∠AED = ∠AFD = 90°，所以四边形AEDF是矩形，由②得DE = DF，所以四边形AEDF是正方形，所以③正确；④因为AE = AF，DE = DF，所以AE² + DF² = AF² + DE²，所以④正确. 故选D.