第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
11(原创题)如图,点$P$为直线$y = -\frac{4}{3}x + 4$上的一动点,连接$OP$,则( )
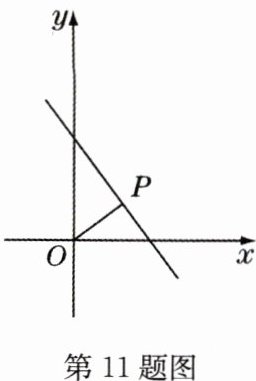
A. $OP$有最大值为4
B. $OP$有最小值为3
C. $OP$有最大值为$\frac{24}{5}$
D. $OP$有最小值为$\frac{12}{5}$

A. $OP$有最大值为4
B. $OP$有最小值为3
C. $OP$有最大值为$\frac{24}{5}$
D. $OP$有最小值为$\frac{12}{5}$
答案:
D 解析:设直线y = -4/3x + 4与x轴的交点为点A,与y轴的交点为点B,令y = 0,则-4/3x + 4 = 0,解得x = 3,
∴点A的坐标为(3,0)。 令x = 0,解得y = 4,
∴点B的坐标为(0,4),
∴OA = 3,OB = 4,
∴由勾股定理得AB = 5。当OP⊥AB时,OP的值最小。利用三角形面积可得OP = 12/5。
∴点A的坐标为(3,0)。 令x = 0,解得y = 4,
∴点B的坐标为(0,4),
∴OA = 3,OB = 4,
∴由勾股定理得AB = 5。当OP⊥AB时,OP的值最小。利用三角形面积可得OP = 12/5。
12 在直线$y = \frac{1}{2}x + \frac{1}{2}$上,到$x$轴或$y$轴的距离为1的点有( )
A. 1个
B. 2个
C. 3个
D. 4个
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
13 将直线$y = 2x + 1$先向上平移3个单位,再向左平移2个单位,则平移后所得直线的解析式为__________.
答案:
y = 2x + 8
14 正方形$A_1B_1C_1O,A_2B_2C_2C_1,A_3B_3C_3C_2,\cdots$按如图放置,点$A_1,A_2,A_3,\cdots$,和点$C_1,C_2,C_3,\cdots$,分别在直线$y = x + 1$和$x$轴上,则点$C_6$的坐标是________.


答案:
(63,0) 解析:易得点C₁的横坐标为1 = 2¹ - 1;点C₂的横坐标为1 + 2 = 3 = 2² - 1;点C₃的横坐标为1 + 2 + 4 = 7 = 2³ - 1;点C₄的横坐标为1 + 2 + 4 + 8 = 15 = 2⁴ - 1;
∴点C₆的横坐标为2⁶ - 1,
∴点C₆的坐标为(63,0)。
∴点C₆的横坐标为2⁶ - 1,
∴点C₆的坐标为(63,0)。
15 将直线$y = 2x + 1$向上平移3个单位长度,则所得直线与$x$轴,$y$轴围成的图形的面积为________.
答案:
4 解析:把直线y = 2x + 1向上平移3个单位长度可得直线y = 2x + 4。设直线y = 2x + 4与x轴,y轴的交点分别为A,B。
当x = 0时,y = 4,
∴点B的坐标为(0,4)。 当y = 0时,2x + 4 = 0,x = -2,
∴点A的坐标为(-2,0),
∴OA = 2,OB = 4,
∴S△AOB = 1/2×2×4 = 4。
∴点B的坐标为(0,4)。 当y = 0时,2x + 4 = 0,x = -2,
∴点A的坐标为(-2,0),
∴OA = 2,OB = 4,
∴S△AOB = 1/2×2×4 = 4。
16(原创题)如图,直线$y = -\frac{3}{4}x + 3$与$x$轴交于点$A$,与$y$轴交于点$B,M$为线段$AB$上一点,当$\triangle AOM$为等腰三角形时,求点$M$的坐标.
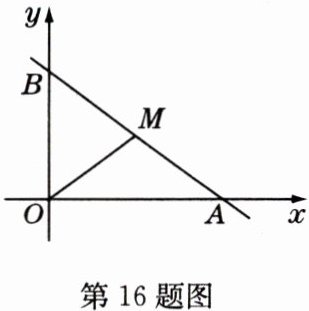

答案:
解:对于直线y = -3/4x + 3, 当y = 0时,解得x = 4,
∴点A的坐标为(4,0)。当x = 0时,解得y = 3,
∴点B的坐标为(0,3)。
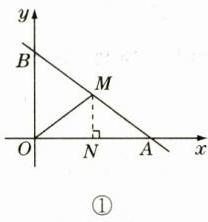
①当MO = MA时,作MN⊥OA于点N,如图①,则ON = AN = 2。把x = 2代入y = -3/4x + 3,得y = 3/2。
∴点M的坐标为(2,3/2)。
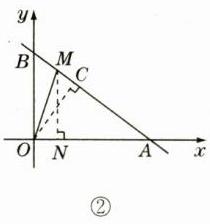
②当AM = AO时,过点M作MN⊥x轴于点N,过点O作OC⊥AB于点C,如图②,易求AB = 5,从而求出OC = 12/5。
∵OA·MN = AM·OC,即4MN = 4×12/5,
∴MN = 12/5。 把y = 12/5代入y = -3/4x + 3,得x = 4/5,
∴点M的坐标为(4/5,12/5)。 综上,点M的坐标为(2,3/2)或(4/5,12/5)。
解:对于直线y = -3/4x + 3, 当y = 0时,解得x = 4,
∴点A的坐标为(4,0)。当x = 0时,解得y = 3,
∴点B的坐标为(0,3)。

①当MO = MA时,作MN⊥OA于点N,如图①,则ON = AN = 2。把x = 2代入y = -3/4x + 3,得y = 3/2。
∴点M的坐标为(2,3/2)。

②当AM = AO时,过点M作MN⊥x轴于点N,过点O作OC⊥AB于点C,如图②,易求AB = 5,从而求出OC = 12/5。
∵OA·MN = AM·OC,即4MN = 4×12/5,
∴MN = 12/5。 把y = 12/5代入y = -3/4x + 3,得x = 4/5,
∴点M的坐标为(4/5,12/5)。 综上,点M的坐标为(2,3/2)或(4/5,12/5)。
17(原创题)如图,把直线${l}_{1}:y=\frac{1}{2}x}$向上平移$\sqrt{5}$个单位长度得到直线${l}_{2}$,直线${l}_{2}$交${y}$轴于点${A}$,${B}$是直线${l}_{2}$上一点,过点${B}$作${x}$轴的垂线,垂足为点${D}$,交${l}_{1}$于点${C}$.
(1)求直线${l}_{2}$的函数解析式.
(2)当四边形${OABC}$为菱形时,求点${B}$的坐标.
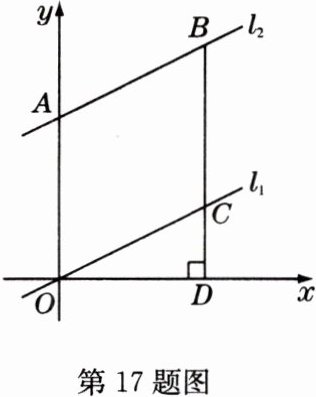
(1)求直线${l}_{2}$的函数解析式.
(2)当四边形${OABC}$为菱形时,求点${B}$的坐标.

答案:
解:
(1)l₂的函数解析式为y = 1/2x + √5。
(2)
∵OA//BC,AB//OC,
∴四边形OABC为平行四边形。 当OA = OC时,四边形OABC为菱形,设点C的坐标为(m,1/2m), 则OC = √(m² + (1/2m)²) = √(5/4m²) = √5/2m。 又
∵OA = √5,
∴√5/2m = √5,
∴m = 2,
∴点C的坐标为(2,1)。 又
∵BC = OA = √5,
∴点B的坐标为(2,√5 + 1)。
(1)l₂的函数解析式为y = 1/2x + √5。
(2)
∵OA//BC,AB//OC,
∴四边形OABC为平行四边形。 当OA = OC时,四边形OABC为菱形,设点C的坐标为(m,1/2m), 则OC = √(m² + (1/2m)²) = √(5/4m²) = √5/2m。 又
∵OA = √5,
∴√5/2m = √5,
∴m = 2,
∴点C的坐标为(2,1)。 又
∵BC = OA = √5,
∴点B的坐标为(2,√5 + 1)。
查看更多完整答案,请扫码查看


