《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

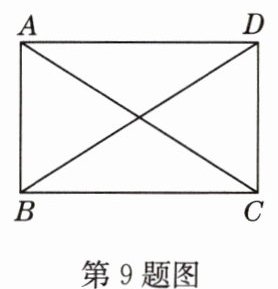
9 (原创题)如图，在四边形ABCD中，已知∠BCD = ∠ADC = 90°，若添加下列条件中的一个条件：①∠DAC = 90°；②∠CBA = 90°；③AB//CD；④AC = BD，使得四边形ABCD是矩形，则可以添加的有（ ）


A. 1个
B. 2个
C. 3个
D. 4个

答案： B

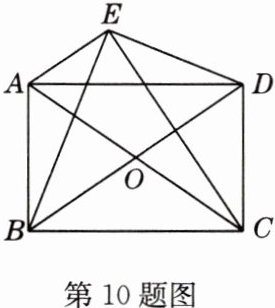
10 如图，四边形ABCD中，对角线AC，BD相交于点O，已知AD//BC，AO = CO.
(1)求证：四边形ABCD为平行四边形.
(2)E是四边形ABCD外一点，且∠AEC = ∠BED = 90°，求证：四边形ABCD为矩形.

答案： 证明：
(1)
∵AD//BC，
∴∠DAO = ∠BCO。又∠AOD = ∠COB，AO = CO，
∴△AOD≌△COB，
∴AD = BC，
∴四边形ABCD为平行四边形。
(2)连接EO。
∵∠AEC = 90°，AO = CO，
∴EO = 1/2AC。
∵∠BED = 90°，BO = DO，
∴EO = 1/2BD，
∴AC = BD。又四边形ABCD为平行四边形，
∴平行四边形ABCD为矩形。

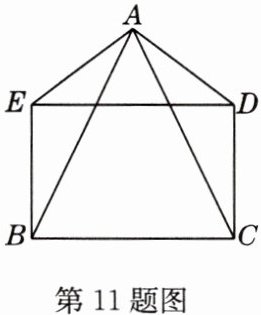
11 如图，已知AB = AC，AD = AE，DE = BC，且∠BAD = ∠CAE，求证：四边形BCDE为矩形.

答案： 证明：
∵∠BAD = ∠CAE，
∴∠BAE = ∠CAD。又AB = AC，AE = AD，
∴△ABE≌△ACD，
∴BE = CD。又DE = BC，
∴四边形BCDE为平行四边形，
∴EB//CD，
∴∠EBC + ∠DCB = 180°。
∵AB = AC，
∴∠ABC = ∠ACB。
∵△ABE≌△ACD，
∴∠ABE = ∠ACD，
∴∠EBC = ∠DCB = 90°，
∴平行四边形BCDE为矩形。

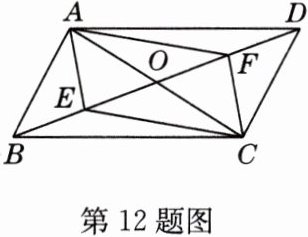
12 如图，在□ABCD中，AC = 8 cm，BD = 12 cm，点E，F在对角线BD上，点E从点B出发向点D运动，同时点F从点D出发向点B运动，到端点停止，运动速度均为2 cm/s，运动时间为t s.
(1)求证：四边形AECF为平行四边形.
(2)求当t为何值时，四边形AECF为矩形.

答案：
(1)证明：
∵四边形ABCD是平行四边形，
∴AO = CO，BO = DO，由题意可知BE = DF，
∴EO = FO，
∴四边形AECF为平行四边形。
(2)解：情况一：当0≤t≤3时，OE = OF = OA = OC = 4 cm，四边形AECF为矩形。此时，2t = 2，t = 1。 情况二：当3＜t≤6时。OE = OF = OA = OC = 4 cm，四边形AECF为矩形，此时，2t = 10，t = 5。
∴当t = 1或t = 5时，四边形AECF为矩形。

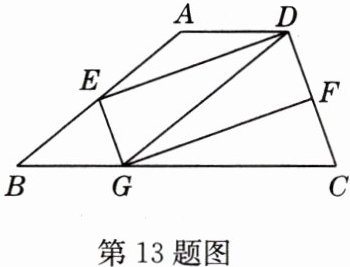
13 如图，四边形ABCD中，AD//BC, E、F分别是AB, CD的中点，点G在BC边上，且CG=$\frac{1}{2}(AD + BC)$.
(1)求证：四边形DEGF是平行四边形.
(2)连接DG,若∠ADG = 2∠ADE. 求证：四边形DEGF是矩形.

答案： 证明：
(1)延长DE交CB的延长线于点H。
∵AD//BC，
∴∠H = ∠1。
∵E为AB中点，
∴AE = BE。又
∵∠AED = ∠BEH，
∴△ADE≌△BHE，
∴DE = HE，AD = BH，
∴CG = 1/2(AD + BC) = 1/2(BH + BC) = 1/2CH，
∴HG = CG。又DE = HE，
∴EG//DF。又F为CD的中点，
∴FG//DE，
∴四边形DEGF为平行四边形。
(2)
∵∠ADG = 2∠ADE，
∴∠1 = ∠2。又∠1 = ∠H，
∴∠2 = ∠H，
∴GH = GD。又CG = GH，
∴CG = DG，
∴∠3 = ∠C。
∵∠H + ∠2 + ∠3 + ∠C = 180°，
∴∠2 + ∠3 = 90°，即∠EDF = 90°，
∴平行四边形DEGF为矩形。