第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
12 (易错题)在△ABC中,∠A、∠B、∠C所对的边分别为a,b,c,若a + b = 4,ab = 1,c = √14,则△ABC是( )
A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 等腰直角三角形
A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 等腰直角三角形
答案:
B 解析:(a + b)² = 4²,a² + 2ab + b² = 16,
又ab = 1,
∴a² + b² = 14, 又c = √14,
∴c² = 14.
∴a² + b² = c²,
∴△ABC是直角三角形。
∴a² + b² = 14, 又c = √14,
∴c² = 14.
∴a² + b² = c²,
∴△ABC是直角三角形。
13 如图,在四边形ABCD中,∠ABC = 90°,若AB = 1,BC = 2,CD = √5,AD = √10,则BD的长为_______.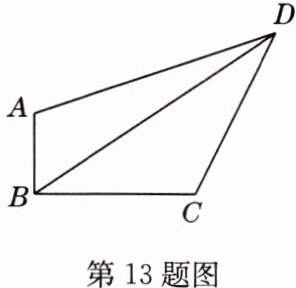

答案:
√13 解析:作DM⊥BC,交BC的延长线于点M,连接AC,如图所示,则∠M = 90°,
∴∠DCM + ∠CDM = 90°。
∵∠ABC = 90°,AB = 1,BC = 2,
∴AC² = AB² + BC² = 5,
∴AC = √5。
∵CD = √5,AD = √10,
∴AC² + CD² = AD²,
∴△ACD是等腰直角三角形,∠ACD = 90°,AC = CD,
∴∠ACB + ∠DCM = 90°,
∴∠ACB = ∠CDM,
∵∠ABC = ∠M = 90°,AC = CD,
∴△ABC≌△CMD.
∴CM = AB = 1,DM = CB = 2,
∴BM = 2 + 1 = 3,
∴BD = √BM² + DM² = √13。
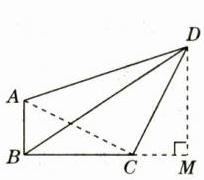
√13 解析:作DM⊥BC,交BC的延长线于点M,连接AC,如图所示,则∠M = 90°,
∴∠DCM + ∠CDM = 90°。
∵∠ABC = 90°,AB = 1,BC = 2,
∴AC² = AB² + BC² = 5,
∴AC = √5。
∵CD = √5,AD = √10,
∴AC² + CD² = AD²,
∴△ACD是等腰直角三角形,∠ACD = 90°,AC = CD,
∴∠ACB + ∠DCM = 90°,
∴∠ACB = ∠CDM,
∵∠ABC = ∠M = 90°,AC = CD,
∴△ABC≌△CMD.
∴CM = AB = 1,DM = CB = 2,
∴BM = 2 + 1 = 3,
∴BD = √BM² + DM² = √13。

14 (2022·咸宁)勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;….这类勾股数的特点是勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是_______(结果用含m的式子表示).
答案:
m² + 1 解析:2m为偶数,设股为a,则弦为a + 2.
由勾股定理得a² + (2m)² = (a + 2)²,
解得a = m² - 1,
所以弦是m² + 1.
15 如图,在四边形ABCD中,∠D = 90°,AB = 2,BC = 4,CD = AD = √6.
(1)求∠BAD的度数;
(2)求四边形ABCD的面积.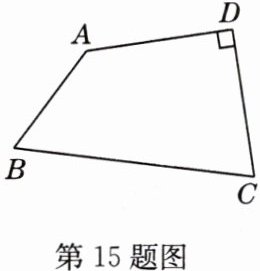
(1)求∠BAD的度数;
(2)求四边形ABCD的面积.

答案:
解:
(1)连接AC.在Rt△ADC中,AC² = AD² + CD² = (√6)² + (√6)² = 6 + 6 = 12,
∴AC = √12 = 2√3。在△ABC中,
∵AB² + AC² = 2² + (2√3)² = 4 + 12 = 16,BC² = 4² = 16,
∴AB² + AC² = BC²,
∴∠BAC = 90°。
∵∠D = 90°,CD = AD,
∴∠DAC = 45°,
∴∠BAD = 135°。
(2)S四边形ABCD = S△ABC + S△ACD = 1/2×2×2√3 + 1/2×√6×√6 = 2√3 + 3.
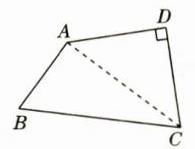
解:
(1)连接AC.在Rt△ADC中,AC² = AD² + CD² = (√6)² + (√6)² = 6 + 6 = 12,
∴AC = √12 = 2√3。在△ABC中,
∵AB² + AC² = 2² + (2√3)² = 4 + 12 = 16,BC² = 4² = 16,
∴AB² + AC² = BC²,
∴∠BAC = 90°。
∵∠D = 90°,CD = AD,
∴∠DAC = 45°,
∴∠BAD = 135°。
(2)S四边形ABCD = S△ABC + S△ACD = 1/2×2×2√3 + 1/2×√6×√6 = 2√3 + 3.

16 如图,在△ABC中,CD是高,已知CD² = AD·BD,求证:△ABC是直角三角形.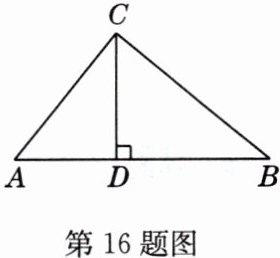

答案:
证明:
∵CD是高,
∴∠ADC = ∠BDC = 90°。在Rt△ACD中,AC² = AD² + CD²。在Rt△BCD中,BC² = BD² + CD²。在△ABC中,
∵AC² + BC² = AD² + CD² + BD² + CD² = AD² + 2CD² + BD² = AD² + 2AD·BD + BD² = (AD + BD)² = AB²,
∴△ABC是直角三角形。
∵CD是高,
∴∠ADC = ∠BDC = 90°。在Rt△ACD中,AC² = AD² + CD²。在Rt△BCD中,BC² = BD² + CD²。在△ABC中,
∵AC² + BC² = AD² + CD² + BD² + CD² = AD² + 2CD² + BD² = AD² + 2AD·BD + BD² = (AD + BD)² = AB²,
∴△ABC是直角三角形。
17 (探究题)如图,CD是△ABC的高,AD = 9,BD = 16,问:当高CD为多少时,△ABC是直角三角形?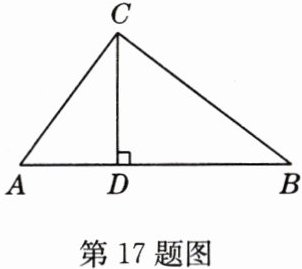

答案:
解:当AC² + BC² = AB²时,△ABC是直角三角形。
∵CD是高,
∴∠ADC = ∠BDC = 90°。设CD = x,在Rt△ACD中,AC² = AD² + CD² = 9² + x² = x² + 81;在Rt△BCD中,BC² = BD² + CD² = 16² + x² = x² + 256。 代入AC² + BC² = AB²,得x² + 81 + x² + 256 = (9 + 16)²,解得x = 12. 即当CD = 12时,△ABC是直角三角形。
∵CD是高,
∴∠ADC = ∠BDC = 90°。设CD = x,在Rt△ACD中,AC² = AD² + CD² = 9² + x² = x² + 81;在Rt△BCD中,BC² = BD² + CD² = 16² + x² = x² + 256。 代入AC² + BC² = AB²,得x² + 81 + x² + 256 = (9 + 16)²,解得x = 12. 即当CD = 12时,△ABC是直角三角形。
18 (原创题)如图,在△ABC中,AC = BC,D,E为AB边上的两点,且∠DCE = 1/2∠ACB,AD² + BE² = DE²,求证:△ABC为等腰直角三角形.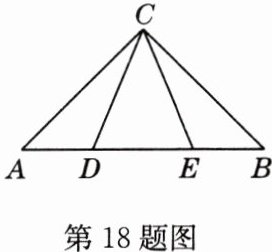

答案:
证明:作△BCF≌△ACD,如图所示。连接EF.
∵∠DCE = 1/2∠ACB,
∴∠ACD + ∠BCE = ∠DCE。又
∵∠ACD = ∠BCF,
∴∠BCF + ∠BCE = ∠DCE,即∠FCE = ∠DCE. 在△DCE和△FCE中,{CD = CF,∠DCE = ∠FCE,CE = CE},
∴△DCE≌△FCE,
∴DE = FE.
∵AD² + BE² = DE²,
∴BF² + BE² = EF²,
∴△BEF是直角三角形,
∴∠EBF = 90°。即∠CBA + ∠CBF = 90°。又∠A = ∠CBF,
∴∠CBA + ∠A = 90°,
∴∠ACB = 90°。又AC = BC,
∴△ABC是等腰直角三角形。
证明:作△BCF≌△ACD,如图所示。连接EF.
∵∠DCE = 1/2∠ACB,
∴∠ACD + ∠BCE = ∠DCE。又
∵∠ACD = ∠BCF,
∴∠BCF + ∠BCE = ∠DCE,即∠FCE = ∠DCE. 在△DCE和△FCE中,{CD = CF,∠DCE = ∠FCE,CE = CE},
∴△DCE≌△FCE,
∴DE = FE.
∵AD² + BE² = DE²,
∴BF² + BE² = EF²,
∴△BEF是直角三角形,
∴∠EBF = 90°。即∠CBA + ∠CBF = 90°。又∠A = ∠CBF,
∴∠CBA + ∠A = 90°,
∴∠ACB = 90°。又AC = BC,
∴△ABC是等腰直角三角形。

查看更多完整答案,请扫码查看


