第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
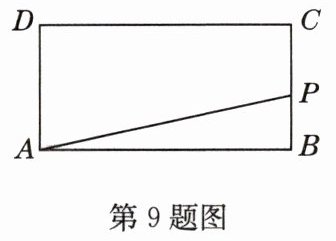
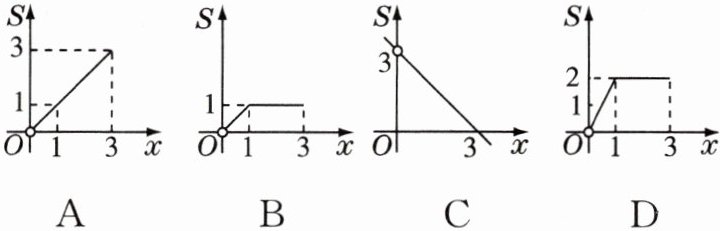
9 如图,在矩形ABCD中,AB = 2,BC = 1,动点P从B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间大致的函数图象是 ( )


答案:
B 解析:当$0 < x \leq 1$时,S随x的增大而增大;当$1 < x \leq 3$时,S的值不变,为1。
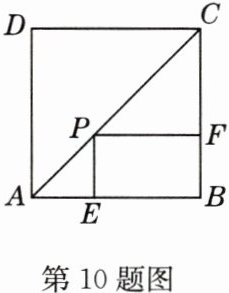
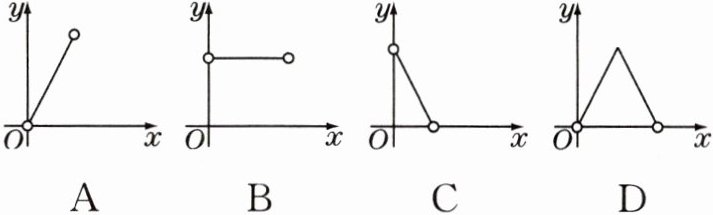
10 如图,P是边长为1的正方形ABCD的对角线AC上一动点(不与端点重合),由点A向点C运动,过点P分别向AB和CB作垂线,垂足分别为E,F,设点P运动的路程为x,矩形PEBF的周长为y,则y与x的函数图象为 ( )


答案:
B 解析:由四边形ABCD为正方形可知$PE = AE$,$PF = CF$。$\therefore$四边形PEBF的周长为$PE + BE + PF + BF = AE + BE + CF + BF = AB + BC = 1 + 1 = 2$。
11 一列有规律的数:0,3,8,15,24,35,….设第n个数是m,则m与n的函数解析式为_________.
答案:
$m = n^{2} - 1$
12 一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水至12分钟关停进水管,在打开进水管到关停进水管这段时间内容器内的水量y(升)与时间x(分)之间的函数关系如图所示,关停进水管后,经过_________分钟,容器中的水正好放完.
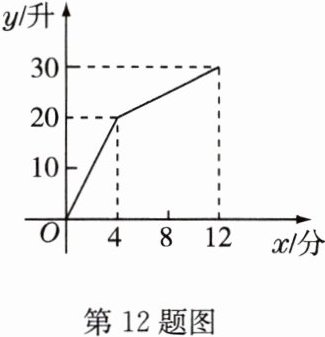

答案:
8 解析:每分钟进水20÷4 = 5(升),设每分钟放水m升,则30 - 20 = 8×5 - 8m,解得$m = \frac{15}{4}$。$\therefore 30 \div \frac{15}{4} = 8$(分)。
13 图①中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图②所示.
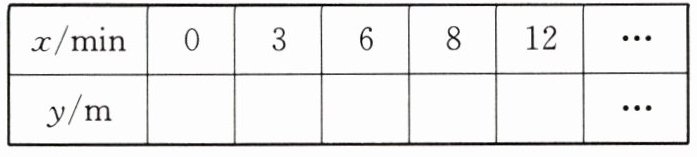
(1)根据图②填表:
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
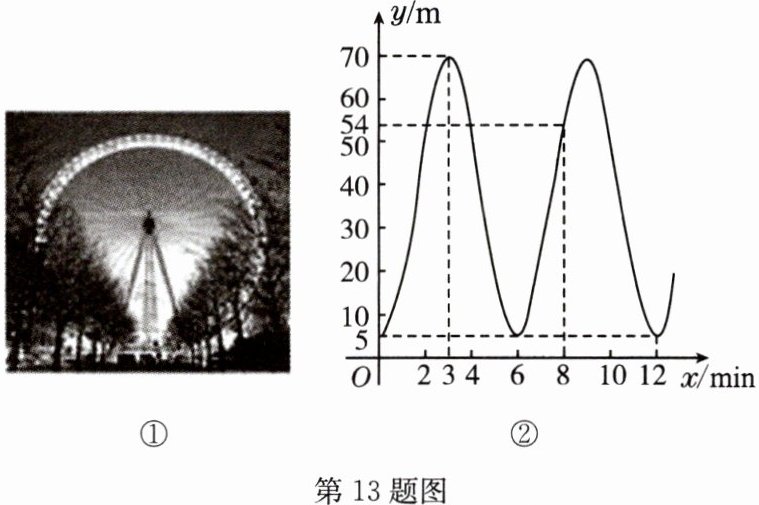
(1)根据图②填表:

(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.

答案:
解:
(1)表格中分别填写:5,70,5,54,5。
(2)变量y是x的函数。 理由:因为在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与其对应,所以变量y是x的函数。
(3)摩天轮的直径是70 - 5 = 65(m)。
(1)表格中分别填写:5,70,5,54,5。
(2)变量y是x的函数。 理由:因为在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与其对应,所以变量y是x的函数。
(3)摩天轮的直径是70 - 5 = 65(m)。
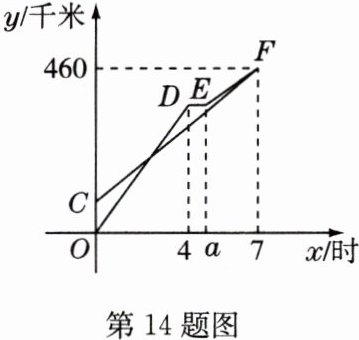
14 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速行驶40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲、乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,有下列说法:①a = 4.5;②甲的速度是60千米/时;③乙出发80分钟追上甲;④乙刚到达货站时,甲距B地180千米.其中正确的有 ( )
A. 1个
B. 2个
C. 3个
D. 4个

A. 1个
B. 2个
C. 3个
D. 4个
答案:
D 解析:线段DE表示乙车在途中的货站耗时半小时,$\therefore a = 4 + 0.5 = 4.5$,即①正确;40分$ = \frac{2}{3}$时,甲车的速度为$460 \div (7 + \frac{2}{3}) = 60$(千米/时),即②正确;设乙车刚出发时的速度为x千米/时,则装满货后的速度为(x - 50)千米/时,根据题意可知,$4x + (7 - 4.5)(x - 50) = 460$,解得$x = 90$,乙车发车时,甲车行驶的路程为$60 \times \frac{2}{3} = 40$(千米),乙车追上甲车的时间为$40 \div (90 - 60) = \frac{4}{3}$(时),$\frac{4}{3}$时 = 80分,即③正确;乙车刚到达货站时,甲车行驶的时间为$(4 + \frac{2}{3})$小时,此时甲车离B地的距离为$460 - 60 \times (4 + \frac{2}{3}) = 180$(千米),即④正确。综上可知,正确的有①②③④,故选D。
查看更多完整答案,请扫码查看


