《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

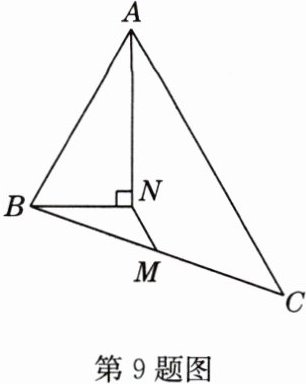
9 如图，在△ABC中，M是BC的中点，AN平分∠BAC，BN⊥AN，若AB = 10，AC = 15，则MN的长为（ ）

A. 2
B. 2.5
C. 3
D. 3.5

答案： B 解析：延长BN交AC于点D。易证△ABN≌△ADN，所以DN = BN，AD = AB = 10，所以CD = AC - AD = AC - AB = 15 - 10 = 5。因为M为BC的中点，N为BD的中点，所以MN是△BCD的中位线，所以$MN = \frac{1}{2}CD = \frac{1}{2}×5 = 2.5$。

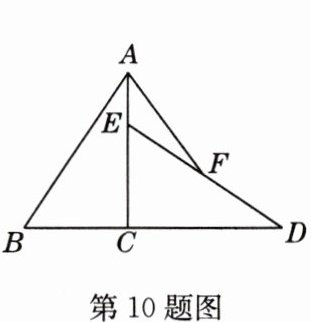
10 如图，Rt△ABC中，∠ACB = 90°，AC = 6，BC = 4，△CDE≌△CAB，其中点E在AC上，F为DE的中点，连接AF，则AF的长是（ ）

A. 4
B. 5
C. 6
D. $4\sqrt{2}$

答案： B 解析：因为△CDE≌△CAB，所以DC = AC = 6，EC = BC = 4。所以AE = 6 - 4 = 2。取CE的中点G，连接FG。因为F为DE的中点，所以GF是△CDE的中位线，所以$GF = \frac{1}{2}CD = \frac{1}{2}×6 = 3$，GF//CD，所以∠EGF = ∠ECD = 90°。又EG = CG = 2，所以AG = AE + EG = 2 + 2 = 4。在Rt△AGF中，$AF = \sqrt{AG^{2}+FG^{2}}=\sqrt{4^{2}+3^{2}} = 5$。

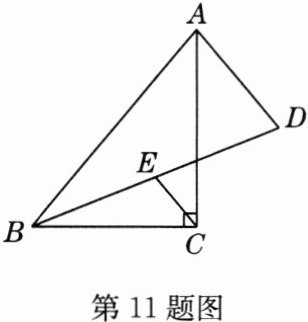
11 如图，在Rt△ABC中，∠ACB = 90°，D为△ABC外一点，∠DAC = ∠BAC，E为BD的中点.若∠ABC = 50°，则∠ACE的度数为______.

答案： 40° 解析：延长AD交BC的延长线于点F。易证△ABC≌△AFC，所以BC = FC。又E为BD中点，所以CE为△BFD的中位线，所以CE//FD，所以∠ECB = ∠F。又∠F = ∠ABC = 50°，所以∠ECB = 50°。又∠ACB = 90°，所以∠ACE = 90° - 50° = 40°。

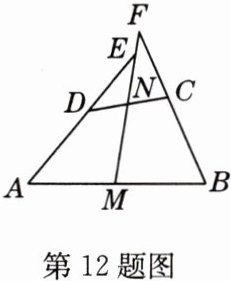
12 如图所示，在四边形ABCD中，AD = BC，M，N分别为AB，CD的中点，AD，BC的延长线分别交MN的延长线于点E，F.求证：∠DEN = ∠F.

答案： 证明：如图，连接AC，取AC的中点G，连接MG，NG。因为M，N分别是AB，CD的中点，所以NG，MG分别是△CAD和△ABC的中位线，所以$NG\underline{\underline{//}}\frac{1}{2}AD$，$MG\underline{\underline{//}}\frac{1}{2}BC$。因为AD = BC，所以NG = GM，所以∠GNM = ∠GMN。因为GM//BF，所以∠GMF = ∠F。因为GN//AD，所以∠GNM = ∠DEN。所以∠DEN = ∠F。

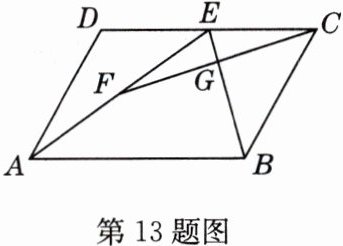
13 已知，如图，在□ABCD中，点E是CD的中点，点F是AE的中点，FC与BE相交于点G.求证：GF = GC.

答案： 证明：取BE的中点H，连接FH，CH。因为四边形ABCD为平行四边形，所以$CD\underline{\underline{//}}AB$。又E为CD的中点，所以$CE\underline{\underline{//}}\frac{1}{2}AB$。因为F，H分别为AE，BE的中点，所以FH是△ABE的中位线，所以$FH\underline{\underline{//}}\frac{1}{2}AB$，所以$CE\underline{\underline{//}}FH$，所以四边形EFHC为平行四边形，所以GF = GC。

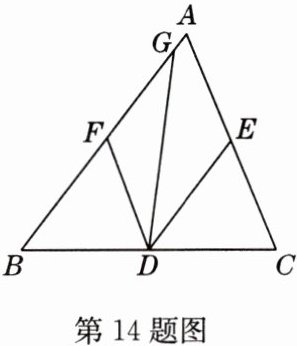
14 如图，△ABC中，D，E，F分别为三边的中点，点G在边AB上，且△BDG与四边形ACDG的周长相等，设BC = a，AC = b，AB = c.
（1）求线段BG的长.（用含a,b,c的式子表示）
（2）求证：DG平分∠EDF.

答案： （1）解：因为△BDG与四边形ACDG的周长相等，所以BG + BD = AG + AC + CD。又因为D为BC中点，所以BD = CD，所以BG = AG + AC = AB - BG + AC，所以2BG = AB + AC = c + b。所以$BG = \frac{b + c}{2}$。 （2）证明：因为D，F分别为BC，BA的中点，所以DF是△ABC的中位线。所以$DF = \frac{1}{2}AC = \frac{1}{2}b$。又$FG = BG - BF = \frac{b + c}{2}-\frac{1}{2}c = \frac{1}{2}b$，所以DF = GF，所以∠FDG = ∠FGD。因为DE//AB，所以∠FGD = ∠EDG，所以∠FDG = ∠EDG，所以DG平分∠EDF。