《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

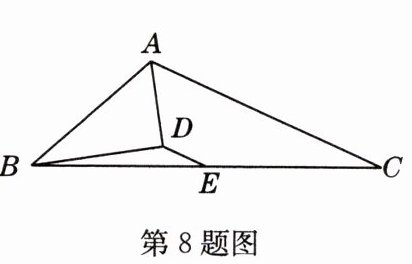
8 如图，在△ABC中，E为BC的中点，AD平分∠BAC，BD⊥AD，若AB = 10，AC = 16，则DE =________.

答案： 3 - **解析**：延长BD交AC于点H，如图。在△ADB和△ADH中，$\begin{cases}\angle BAD=\angle HAD\\AD = AD\\\angle ADB=\angle ADH\end{cases}$，所以△ADB≌△ADH(ASA)，所以AH = AB = 10，BD = DH，所以HC = AC - AH = 6，因为BD = DH，BE = EC，所以DE为△BCH的中位线，所以DE = $\frac{1}{2}$HC = 3。

9 如图，已知△ABC，分别以△ABC的三边为边在△ABC的同侧作三个等边三角形：△ABE，△BCD，△ACF，连接DE，DF，求证：四边形DEAF是平行四边形.

答案： 证明：因为△ABE，△BDC都是等边三角形，所以BE = AB，BD = BC，∠EBA = ∠DBC = 60°，所以∠DBE = 60° - ∠DBA，∠ABC = 60° - ∠DBA，所以∠DBE = ∠ABC。在△DBE和△CBA中，$\begin{cases}BE = BA\\\angle DBE=\angle CBA\\BD = BC\end{cases}$，所以△DBE≌△CBA(SAS)，所以DE = AC。又因为△ACF是等边三角形，所以AC = AF，所以DE = AF。同理可得△ABC≌△FDC，所以DF = AB = AE。因为DE = AF，EA = DF，所以四边形DEAF为平行四边形。

10（2022·扬州）如图，在□ABCD中，BE，DG分别平分∠ABC，∠ADC，交AC于点E，G.
（1）求证：BE//DG，BE = DG.
（2）过点E作EF⊥AB，垂足为F. 若□ABCD的周长为56，EF = 6，求△ABC的面积.

答案： -
(1) **证明**：在□ABCD中，因为AB//CD，所以∠BAE = ∠DCG，因为BE，DG分别平分∠ABC，∠ADC，∠ABC = ∠ADC，所以∠ABE = ∠CDG，在△ABE和△CDG中，$\begin{cases}\angle BAE=\angle DCG\\AB = CD\\\angle ABE=\angle CDG\end{cases}$，所以△ABE≌△CDG(ASA)，所以BE = DG，∠AEB = ∠CGD，所以BE//DG。 -
(2) **解**：如图，作EQ⊥BC于Q，因为□ABCD的周长为56，所以AB + BC = 28，因为BE平分∠ABC，所以EQ = EF = 6，所以$S_{\triangle ABC}$ = $S_{\triangle ABE}$ + $S_{\triangle EBC}$ = $\frac{1}{2}$EF·AB + $\frac{1}{2}$EQ·BC = 3(AB + BC) = 84。

11 如图，平行四边形ABCD中，对角线AC = 21 cm，BE⊥AC，垂足为E，且BE = 5 cm，AD = 7 cm，求AD和BC之间的距离.

答案： 解：设AD和BC之间的距离为x cm，则平行四边形ABCD的面积等于AD·x。因为$S_{平行四边形ABCD}$ = 2$S_{\triangle ABC}$ = 2×$\frac{1}{2}$AC·BE = AC·BE，所以AD·x = AC·BE，即7x = 21×5，解得x = 15。所以AD和BC之间的距离为15 cm。 - **名师点睛**：本题主要考查平行四边形的性质，由条件得到平行四边形ABCD的面积是△ABC面积的2倍是解题的关键，再借助等积法求解使解题事半功倍。

12 如图，四边形ABCD是平行四边形，连接对角线AC，AE⊥BC于点E，F为EA延长线上一点，且BE = EF，连接CF.
（1）如图①，若AB⊥AC，AB = 4，AC = 3，求AF的长度；
（2）如图②，若CD⊥CF，求证：AD=$\sqrt{2}AC + AF$.

答案： -
(1) **解**：因为AB⊥AC，AE⊥BC，所以∠BAC = ∠AEB = 90°，BC = $\sqrt{AB^{2}+AC^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5。由△ABC的面积得AE = $\frac{AB×AC}{BC}$ = $\frac{12}{5}$，所以EF = BE = $\sqrt{AB^{2}-AE^{2}}$ = $\sqrt{4^{2}-(\frac{12}{5})^{2}}$ = $\frac{16}{5}$，所以AF = EF - AE = $\frac{16}{5}$ - $\frac{12}{5}$ = $\frac{4}{5}$。 -
(2) **证明**：因为四边形ABCD是平行四边形，所以∠B = ∠D，BC//AD。因为AE⊥BC，所以AE⊥AD，所以∠DAF = 90°。因为CD⊥CF，所以∠DCF = 90°，所以∠F = ∠D = ∠B。在△ABE和△CFE中，$\begin{cases}\angle AEB=\angle CEF = 90°\\BE = FE\\\angle B=\angle F\end{cases}$，所以△ABE≌△CFE(ASA)，所以AE = CE，所以△ACE是等腰直角三角形，所以AE = $\frac{\sqrt{2}}{2}$AC。因为AD = BC = BE + CE = EF + AE = AF + 2AE，所以AD = $\sqrt{2}$AC + AF。

13（核心素养题）如图所示，在四边形ABCD中，CD＞AB，AB与CD不平行，E，F分别是AC，BD的中点. 求证：EF＞$\frac{1}{2}(CD - AB)$.

答案： 证明：取AD中点G，连接EG，FG。在△ACD中，EG是它的中位线（已知E是AC的中点），所以EG = $\frac{1}{2}$CD①。同理，由F，G分别是BD和AD的中点，从而得到FG是△ABD的中位线，所以FG = $\frac{1}{2}$AB②。在△EFG中，EF＞EG - FG。由①②，得EF＞$\frac{1}{2}$(CD - AB)。 - **技巧点拨**：在多边形的不等关系中，容易引发人们联想三角形中边的不等关系。为了产生$\frac{1}{2}$CD及$\frac{1}{2}$AB的线段，应考虑在含CD，AB的三角形中构造中位线。