《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”.
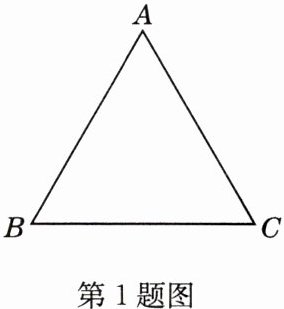
(1)如图，△ABC中，AB = AC = $\sqrt{5}$，BC = 2，求证：△ABC是“美丽三角形”.
(2)在Rt△ABC中，∠C = 90°，AC = 2$\sqrt{3}$，若△ABC是“美丽三角形”，求BC的长.

答案：
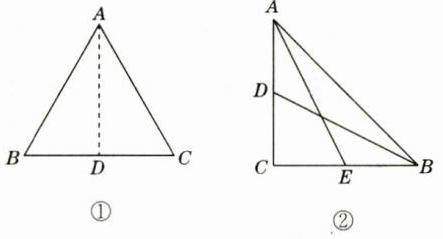
（1）证明：如图①，取BC的中点D，连接AD，则BD = CD = 1，
∵AB = AC，
∴AD⊥BC，在Rt△ABD中，由勾股定理，得$AD=\sqrt{AB^{2}-BD^{2}} = 2$，
∴AD = BC，即△ABC是“美丽三角形”。 （2）解：如图②，当AC边上的中线BD等于AC时，$BC=\sqrt{BD^{2}-CD^{2}} = 3$；当BC边上的中线AE等于BC时，$AC^{2}=AE^{2}-CE^{2}$，即$BC^{2}-(\frac{1}{2}BC)^{2}=(2\sqrt{3})^{2}$，解得BC = 4。综上所述，BC = 3或BC = 4。

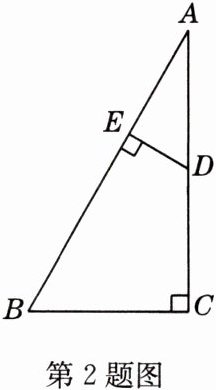
2 如图，在四边形BCDE中，∠C = ∠BED = 90°，∠B = 60°，延长CD，BE得到Rt△ABC，已知CD = 2，DE = 1.
(1)求证：AB = 2BC.
(2)求Rt△ABC的面积.

答案： （1）证明：
∵∠C = 90°，∠B = 60°，
∴∠A = 30°。 在Rt△ABC中，∠C = 90°，∠A = 30°，
∴AB = 2BC。 （2）解：在Rt△ADE中，∠AED = 90°，∠A = 30°，
∴AD = 2DE = 2，
∴AC = AD + DC = 4。 在Rt△ABC中，$AB^{2}=AC^{2}+BC^{2}$，即$4CB^{2}=4^{2}+BC^{2}$，解得$BC=\frac{4\sqrt{3}}{3}$，
∴Rt△ABC的面积为$\frac{1}{2}×4×\frac{4\sqrt{3}}{3}=\frac{8\sqrt{3}}{3}$。

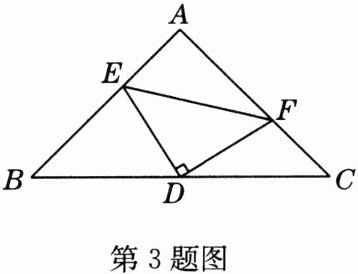
3 已知：如图，在△ABC中，D是BC的中点，E是AB上一点，F是AC上一点.若∠EDF = 90°，且BE² + FC² = EF². 求证：∠BAC = 90°.

答案： 证明：延长FD到点G，使GD = DF，连接BG，EG。
∵D为BC的中点，
∴BD = CD。
∵在△BDG和△CDF中，BD = CD，∠BDG = ∠CDF，DG = DF，
∴△BDG≌△CDF（SAS），
∴BG = FC，∠C = ∠GBD，
∴BG//AC。
∵ED⊥DF，
∴EG = EF。
∵$BE^{2}+FC^{2}=EF^{2}$，
∴$BG^{2}+BE^{2}=EG^{2}$，
∴∠ABG = 90°。
∵BG//AC，
∴∠A + ∠ABG = 180°，
∴∠BAC = 90°。

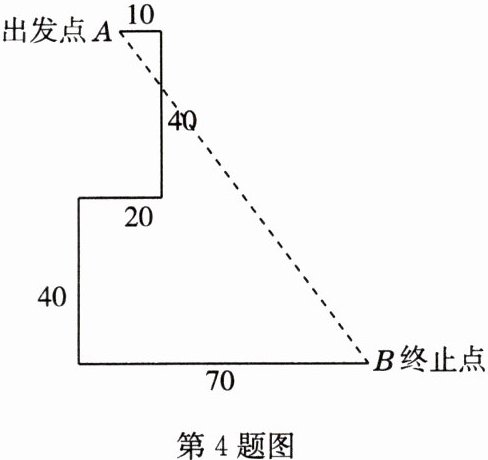
4 如图，某校科技创新兴趣小组用他们设计的机器人，在平坦的操场上进行行走展示. 输入指令后，机器人从出发点A先向东走10米，又向南走40米，再向西走20米，又向南走40米，再向东走70米到达终止点B.求终止点B与原出发点A的距离AB.

答案：
解：如图所示，过点A作AC⊥BD于点C，则在Rt△ABC中，AC = 40 + 40 = 80（米），BC = 70 - 20 + 10 = 60（米），故终止点与原出发点的距离$AB=\sqrt{60^{2}+80^{2}} = 100$（米）。