《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 下列函数中，不是一次函数的是 （ ）
A. $y = 3x$
B. $y = x + 3$
C. $y = \frac{3}{x}$
D. $y = \frac{x}{3}$

答案： C

2 已知关于$x$的函数$y=(m + 1)x^{|m|}+2m$，若$y$是$x$的一次函数，则$m$的值为 （ ）
A. 1
B. -1
C. 0
D. -1或1

答案： A 解析：由题意，得|m| = 1，
∴m = ±1。又
∵m + 1 ≠ 0，
∴m ≠ -1，
∴m = 1。

3（2022·沈阳）在平面直角坐标系中，一次函数$y=-x + 1$的图象是 （ ）

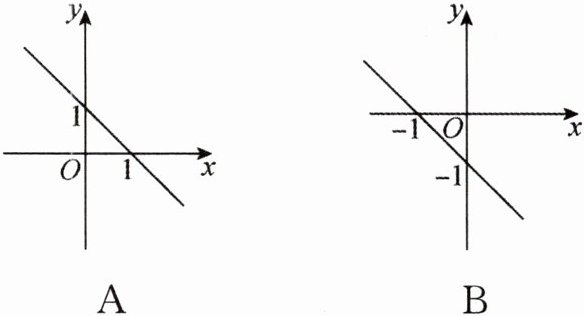
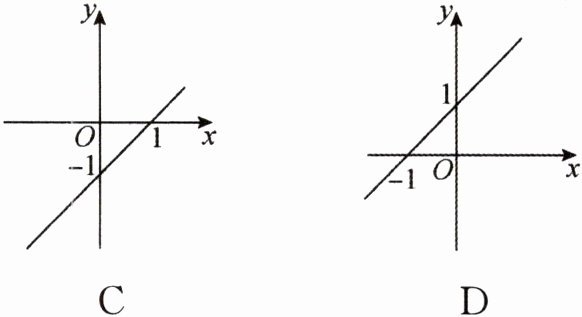
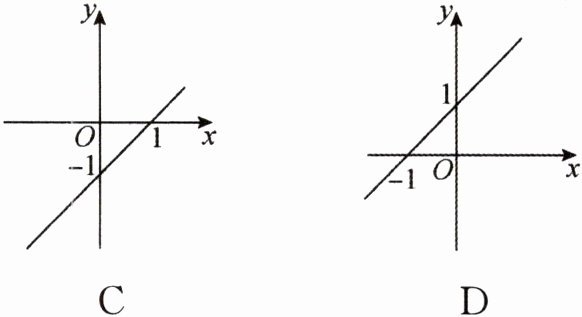
答案： A

4 点$A(1,m)$为直线$y = 2x - 1$上的一点，则$OA$的长为 （ ）
A. 1
B. $\sqrt{3}$
C. $\sqrt{2}$
D. $\sqrt{5}$

答案： C 解析：把点A的坐标x = 1，y = m代入y = 2x - 1，得m = 2×1 - 1 = 1，
∴点A的坐标为(1,1)。 如图，作AB⊥x轴于点B，连接AO，则OA = √(OB² + AB²) = √(1² + 1²) = √2。

5 若点$M(m,n)$在函数$y = 2x + 1$的图象上，则$2m - n$的值是 （ ）
A. 2
B. -2
C. 1
D. -1

答案： D 解析：把点M的坐标x = m，y = n代入y = 2x + 1，得n = 2m + 1，
∴2m - n = -1。

6（2022·兰州）若一次函数$y = 2x + 1$的图象经过点$(-3,y_1)$，$(4,y_2)$，则$y_1$与$y_2$的大小关系是 （ ）
A. $y_1 ＜ y_2$
B. $y_1 ＞ y_2$
C. $y_1 \leq y_2$
D. $y_1 \geq y_2$

答案： A 解析：
∵一次函数y = 2x + 1中，k = 2 ＞ 0，
∴y随着x的增大而增大。
∵点(-3,y₁)和(4,y₂)是一次函数y = 2x + 1图象上的两个点，-3 ＜ 4，
∴y₁ ＜ y₂。故选A。

7（2022·上海）已知直线$y = kx + b$经过第一象限且函数值$y$随着$x$的增大而减小，请列举出来这样的一条直线：________.

答案： y = -x + 2(答案不唯一)

8 把正比例函数$y = \frac{1}{2}x$的图象向下平移3个单位长度，所得直线的函数解析式为 （ ）
A. $y = \frac{1}{2}x + 3$
B. $y = \frac{1}{2}x - 3$
C. $y = 3x + 2$
D. $y = 3x - 2$

答案： B

9 下列每组直线中，互相平行的一组是 （ ）
A. $y = x + 2$与$y = -x + 3$
B. $y = \frac{1}{2}x - 1$与$y = 2x - 1$
C. $y = -4x + 3$与$y = 4x + 3$
D. $y = 2x - 1$与$y = 2x + 1$

答案： D

10（经典题）（2022·抚顺）如图，在同一平面直角坐标系中，一次函数$y = k_1x + b_1$与$y = k_2x + b_2$的图象分别为直线$l_1$和直线$l_2$，下列结论正确的是 （ ）

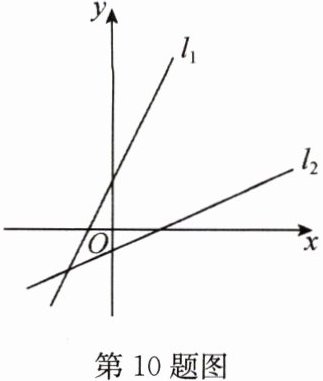
A. $k_1 \cdot k_2 ＜0$
B. $k_1 + k_2 ＜0$
C. $b_1 - b_2 ＜0$
D. $b_1 \cdot b_2 ＜0$

答案： D 解析：一次函数y = k₁x + b₁与y = k₂x + b₂的图象分别为直线l₁和直线l₂，
∴k₁ ＞ 0，b₁ ＞ 0，k₂ ＞ 0，b₂ ＜ 0，
∴k₁·k₂ ＞ 0，k₁ + k₂ ＞ 0，b₁ - b₂ ＞ 0，b₁·b₂ ＜ 0， 故A，B，C项均错误，D项正确。故选D。