《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

13 从高处下落的物体，下落的高度h(米)与下落的时间t(秒)的函数解析式为$h = 4.9t^{2}$，当下落时间$t = 3$时，下落的高度h = _______.

答案： 44.1

14 函数$y = \frac{2}{\sqrt{x + 2}}$中自变量x的取值范围为（ ）
A.$x ＞ -2$
B.$x \geq -2$
C.$x \neq -2$
D.$x \geq -2$

答案： A

15 根据下面所示程序图计算函数值，若输入的x的值为$\frac{5}{2}$，则输出的函数值为（ ）

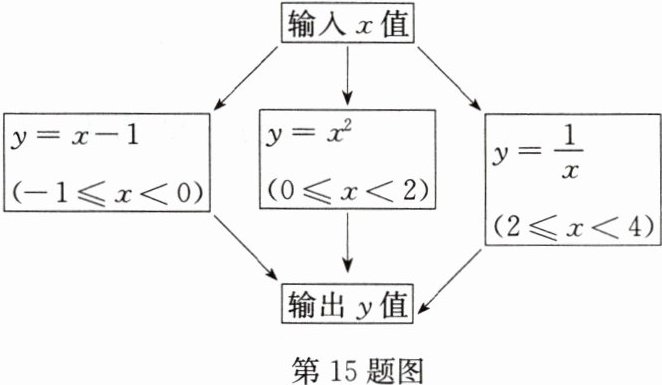
A.$\frac{3}{2}$
B.$\frac{2}{5}$
C.$\frac{4}{25}$
D.$\frac{25}{4}$

答案： B

16 弹簧挂上物体后会伸长，测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间有下面的关系，则下列说法不正确的是（ ）


A.弹簧不挂重物时的长度为0 cm
B.x与y都是变量，且x是自变量，y是自变量的函数
C.物体质量每增加1 kg，弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时，弹簧长度为23.5 cm

答案： A 解析：
∵弹簧不挂重物时的长度为20 cm，
∴选项A说法不正确；
∵x与y都是变量，且x是自变量，y是自变量的函数，
∴选项B说法正确；
∵20.5 - 20 = 0.5(cm)，21 - 20.5 = 0.5(cm)，21.5 - 21 = 0.5(cm)，22 - 21.5 = 0.5(cm)，22.5 - 22 = 0.5(cm)，
∴物体质量每增加1 kg，弹簧长度y增加0.5 cm，
∴选项C说法正确；
∵22.5 + 0.5×(7 - 5)=22.5 + 1 = 23.5(cm)，
∴所挂物体质量为7 kg时，弹簧长度为23.5 cm，
∴选项D说法正确。故选A。

17 在函数$y = \frac{1}{\sqrt{x + 2}} + (x - 2)^{0}$中，自变量x的取值范围是_______.

答案： x ＞ -2且x≠2

18 按如图方式摆放餐桌和椅子.用x来表示餐桌的张数，用y来表示可坐人数.

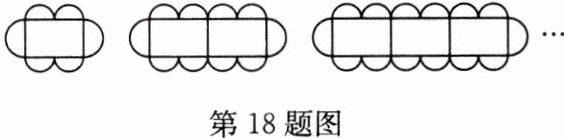
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?

答案： 解：
(1)题中有2个变量，餐桌的数量x和可坐人数y。
(2)能。观察图形：当x = 1时，y = 6；当x = 2时，y = 10；当x = 3时，y = 14；……可见每增加1张桌子，便增加4个座位，因此x张餐桌共有6 + 4(x - 1)=(4x + 2)个座位。故可坐人数y = 4x + 2，函数关系式为y = 4x + 2。

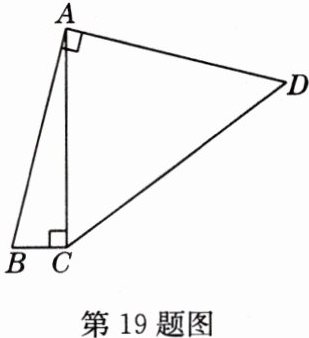
19 如图，在四边形ABCD中，$\angle BAD = \angle ACB =90^{\circ}$，$AB = AD$，$AC = 4BC$，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是什么?

答案：
解：过点D作DE⊥AC于点E，如图。设BC = a，则AC = 4a。
∵∠2 + ∠3 = 90°，∠2 + ∠1 = 90°，
∴∠1 = ∠3。又∠ACB = ∠DEA = 90°，AB = DA，
∴△ABC≌△DAE，
∴AE = BC = a，DE = AC = 4a，
∴EC = AC - AE = 4a - a = 3a。在Rt△DEC中，$DC=\sqrt{DE^{2}+EC^{2}} = 5a$，
∴x = 5a，即$a=\frac{1}{5}x$。又
∵四边形ABCD的面积 = △ABC的面积 + △ACD的面积，
∴$y=\frac{1}{2}×a×4a+\frac{1}{2}×4a×4a = 10a^{2}=\frac{2}{5}x^{2}$，即y与x之间的函数关系式是$y=\frac{2}{5}x^{2}$。