《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

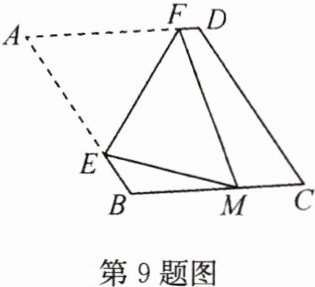
9（2022·台州，难）如图，在菱形ABCD中，∠A = 60°，AB = 6.折叠该菱形，使点A落在边BC上的点M处，折痕分别与边AB，AD交于点E，F.当点M与点B重合时，EF的长为________；当点M的位置变化时，DF长的最大值为________.

答案： $3\sqrt{3}$，$6 - 3\sqrt{3}$\n解析：当点$M$与点$B$重合时，由折叠的性质知$EF$垂直平分$AB$，所以$AE = EB=\frac{1}{2}AB = 3$。\n在$Rt\triangle AEF$中，$\angle A = 60^{\circ}$，$AE = 3$，所以$EF = 3\sqrt{3}$。\n如图，连接$AM$，当$AF$长取得最小值时，$DF$长取得最大值。\n由折叠的性质知$EF$垂直平分$AM$，则$AF = FM$，当$FM\perp BC$时，$FM$长取得最小值，此时$DF$长取得最大值。\n过点$D$作$DG\perp BC$于点$G$，则四边形$DGMF$为矩形，$FM = DG$。\n在$Rt\triangle DGC$中，$\angle C=\angle BAD = 60^{\circ}$，$DC = AB = 6$，所以$DG = 3\sqrt{3}$，$DF$长的最大值为$AD - AF=AD - FM=AD - DG=6 - 3\sqrt{3}$。故答案为$3\sqrt{3}$，$6 - 3\sqrt{3}$。

10（2022·北京，中）如图，在□ABCD中，AC，BD交于点O，点E，F在AC上，AE = CF.
（1）求证：四边形EBFD是平行四边形.
（2）若∠BAC = ∠DAC，求证：四边形EBFD是菱形.

答案： **证明**：\n$(1)$因为四边形$ABCD$为平行四边形，所以$AO = CO$，$BO = DO$。\n因为$AE = CF$，所以$AO - AE=CO - CF$，即$EO = FO$，所以四边形$EBFD$是平行四边形。\n$(2)$因为四边形$ABCD$是平行四边形，所以$AB// CD$，$\angle DCA=\angle BAC$。\n因为$\angle BAC=\angle DAC$，所以$\angle DCA=\angle DAC$，$DA = DC$，所以四边形$ABCD$为菱形，$AC\perp BD$，即$EF\perp BD$。\n因为四边形$EBFD$是平行四边形，所以四边形$EBFD$是菱形。

11（2022·丽水，中）如图，将矩形纸片ABCD折叠，使点B与点D重合，点A落在点P处，折痕为EF.
（1）求证：△PDE≌△CDF.
（2）若CD = 4 cm，EF = 5 cm，求BC的长.

答案： **$(1)$证明**：因为四边形$ABCD$是矩形，所以$AB = CD$，$\angle A=\angle B=\angle ADC=\angle C = 90^{\circ}$。\n由折叠知，$AB = PD$，$\angle A=\angle P$，$\angle B=\angle PDF = 90^{\circ}$，所以$PD = CD$，$\angle P=\angle C$，$\angle PDF=\angle ADC$，$\angle PDF-\angle EDF=\angle ADC-\angle EDF$，即$\angle PDE=\angle CDF$。\n在$\triangle PDE$和$\triangle CDF$中，$\begin{cases}\angle P=\angle C\\PD = CD\\\angle PDE=\angle CDF\end{cases}$，所以$\triangle PDE\cong\triangle CDF(ASA)$。\n**$(2)$解**：如图，过点$E$作$EG\perp BC$于点$G$。\n因为四边形$ABCD$是矩形，所以$AB = CD = EG = 4cm$。\n又因为$EF = 5cm$，所以$GF=\sqrt{EF^{2}-EG^{2}} = 3cm$。\n设$AE = xcm$，所以$EP = xcm$。\n由$\triangle PDE\cong\triangle CDF$知，$EP = CF = xcm$，$DE = GC=GF + FC=(3 + x)cm$。\n在$Rt\triangle PED$中，$PE^{2}+PD^{2}=DE^{2}$，即$x^{2}+4^{2}=(3 + x)^{2}$，解得$x=\frac{7}{6}$。\n所以$BC=BG + GC=\frac{7}{6}+3+\frac{7}{6}=\frac{16}{3}(cm)$。

12（2022·兰州，难）【问题情境】：数学活动课上，老师出示了一个问题：如图①，在正方形ABCD中，E是BC的中点，AE⊥EP，EP与正方形的外角DCG的平分线交于点P.试猜想AE与EP的数量关系，并加以证明.

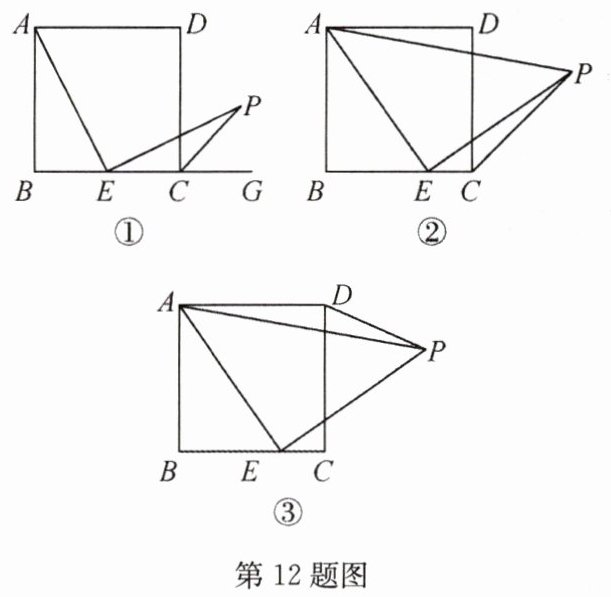
（1）【思考尝试】同学们发现，取AB的中点F,连接EF可以解决这个问题.请在图①中补全图形,解答老师提出的问题.
（2）【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图②,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP = 90°,连接CP,可以求出∠DCP的大小,请你思考并解答这个问题.
（3）【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图③,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP = 90°,连接DP.知道正方形的边长时,可以求出△ADP周长的最小值.当AB = 4时,请你求出△ADP周长的最小值.

答案： **$(1)$ $AE = EP$**\n**理由**：取$AB$的中点$F$，连接$EF$，如图①。\n因为$F$，$E$分别为$AB$，$BC$的中点，所以$AF = BF = BE = CE$，$\angle BFE = 45^{\circ}$，$\angle AFE = 135^{\circ}$。\n因为$CP$平分$\angle DCG$，所以$\angle DCP = 45^{\circ}$，$\angle ECP = 135^{\circ}$，$\angle AFE=\angle ECP$。\n因为$AE\perp PE$，所以$\angle AEP = 90^{\circ}$，$\angle AEB+\angle PEC = 90^{\circ}$。\n又因为$\angle AEB+\angle BAE = 90^{\circ}$，所以$\angle PEC=\angle BAE$，$\triangle AFE\cong\triangle ECP(ASA)$，所以$AE = EP$。\n**$(2)$** 在$AB$上取$AF = EC$，连接$EF$，如图②。\n由$(1)$同理可得$\angle CEP=\angle FAE$。\n因为$AF = EC$，$AE = EP$，所以$\triangle FAE\cong\triangle CEP(SAS)$，$\angle ECP=\angle AFE$。\n因为$AF = EC$，$AB = BC$，所以$BF = BE$，$\angle BEF=\angle BFE = 45^{\circ}$，$\angle AFE = 135^{\circ}$，$\angle ECP = 135^{\circ}$，$\angle DCP = 45^{\circ}$。\n**$(3)$** 作$DG\perp CP$，交$BC$的延长线于点$G$，交$CP$于点$O$，连接$AG$，如图③。\n由$(2)$知，$\angle DCP = 45^{\circ}$，所以$\angle CDG = 45^{\circ}$，$\triangle DCG$是等腰直角三角形，点$D$与点$G$关于直线$CP$对称，$AP + DP$的最小值为$AG$的长。\n因为$AB = 4$，所以$BG = 8$。\n由勾股定理得$AG = 4\sqrt{5}$，$\triangle ADP$周长的最小值为$AD + AG=4 + 4\sqrt{5}$。