《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

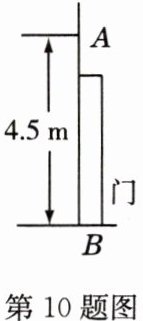
10 如图，有一个由传感器$A$控制的灯，要装在门上方离地面4.5 m的墙上，任何东西只要移至离该灯5 m及5 m内，灯就会自动发光，小明身高1.5 m，他走到离墙______m的地方灯刚好发光.

答案：
4 解析：如图，$AB = 4.5$m，$CD = 1.5$m。平移$CD$到$BE$，则$DE = BC$，$BE = CD = 1.5$m，$\angle AED = 90^{\circ}$，$\therefore AE=AB - BE = 4.5 - 1.5 = 3$（m）。在$Rt\triangle AED$中，$AD = 5$m，$AE^{2}+DE^{2}=AD^{2}$，$\therefore DE^{2}=AD^{2}-AE^{2}=5^{2}-3^{2}=25 - 9 = 16$，$\therefore DE = 4$m，$\therefore BC = 4$m。

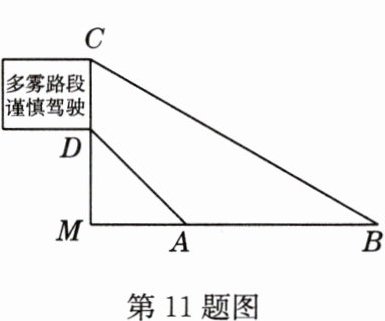
11 如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：$AM = 4$米，$AB = 8$米，$\angle MAD = 45^{\circ}$，$\angle B = 30^{\circ}$.则警示牌的高$CD$为______米.（结果精确到0.1米，$\sqrt{2}\approx1.41,\sqrt{3}\approx1.73$）

答案： 2.9 解析：在$Rt\triangle MBC$中，$\angle B = 30^{\circ}$，$\angle CMB = 90^{\circ}$，$\therefore BC = 2CM$，$MB = MA + AB = 4 + 8 = 12$（米）。设$CM = x$米，由勾股定理得$x^{2}+12^{2}=(2x)^{2}$，解得$x = 4\sqrt{3}$，$\therefore CM = 4\sqrt{3}$米。在$Rt\triangle DMA$中，$\angle MAD = 45^{\circ}$，$\angle AMD = 90^{\circ}$，$\therefore \angle MDA = 45^{\circ}$，$\therefore MD = MA = 4$米，$\therefore DC = CM - MD = 4\sqrt{3}-4\approx4\times1.73 - 4 = 6.92 - 4 = 2.92\approx2.9$（米）。

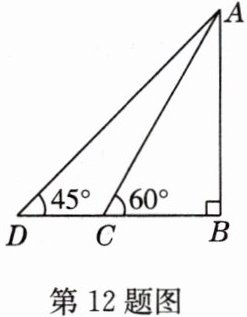
12（经典题）为了测量物体$AB$的高度，在$D$点测得$\angle ADB = 45^{\circ}$，朝物体方向前进20米到达点$C$，再次测得$\angle ACB = 60^{\circ}$，根据测量的数据求物体$AB$的高度.

答案： 解：在$Rt\triangle ABC$中，$\because \angle B = 90^{\circ}$，$\angle ACB = 60^{\circ}$，$\therefore \angle BAC = 30^{\circ}$，$\therefore AC = 2BC$，设$BC = x$米，则$AC = 2x$米。由勾股定理得$AB=\sqrt{AC^{2}-BC^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{4x^{2}-x^{2}}=\sqrt{3x^{2}}=\sqrt{3}x$（米）。在$Rt\triangle ABD$中，$\because \angle D = 45^{\circ}$，$\angle B = 90^{\circ}$，$\therefore \angle BAD=\angle D = 45^{\circ}$，$\therefore AB = BD$，$\therefore \sqrt{3}x=x + 20$，解得$x = 10\sqrt{3}+10$。$\therefore AB=(10\sqrt{3}+30)$米。

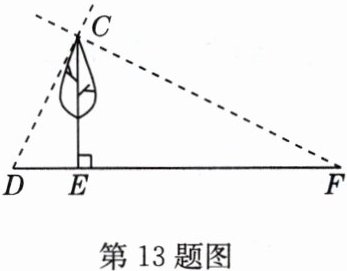
13 如图，小明在$A$时测得某树的影子长$DE$为2 m，$B$时又测得该树的影长$EF$为8 m，若两次日照光线互相垂直，求树高$CE$.

答案： 解：设$CE = x$m，在$Rt\triangle CDE$中，$CD^{2}=CE^{2}+DE^{2}=x^{2}+2^{2}=x^{2}+4$。在$Rt\triangle CEF$中，$CF^{2}=CE^{2}+EF^{2}=x^{2}+8^{2}=x^{2}+64$。在$Rt\triangle CDF$中，$CD^{2}+CF^{2}=DF^{2}$，即$x^{2}+4+x^{2}+64=(2 + 8)^{2}$，解得$x = 4$。$\therefore$树高$CE = 4$m。

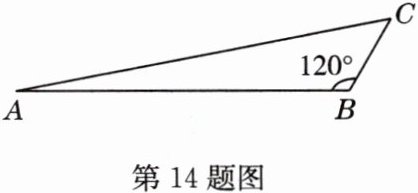
14 从$A$市至$W$市的城际列车已经开通，如下图，以往从$A$市坐客车到$W$市客运站$B$，现在可以在$A$市坐城际列车到$W$市$C$站，再从$W$市$C$站坐市内公共汽车到$W$市客运站$B$，设$AB = 80$km，$BC = 20$km，$\angle ABC = 120^{\circ}$，请你帮助小明解决以下问题：
（1）求$A、C$之间的距离（参考数据：$\sqrt{21}\approx4.6)$．
（2）若客车的平均速度是60 km/h，市内的公共汽车的平均速度为40 km/h，城际列车的平均速度为180 km/h，为了以最短时间从$A$市到达$W$市客运站$B$，小明应该选择哪种乘车方案？请说明理由.（不计候车时间）

答案：
解：
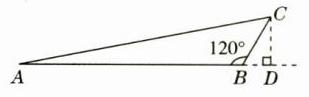
(1)作$CD\perp AB$交$AB$的延长线于点$D$，$\because \angle CBA = 120^{\circ}$，$\therefore \angle CBD = 60^{\circ}$，$\therefore \angle BCD = 30^{\circ}$，$\therefore BD=\frac{1}{2}BC = 10$km，$\therefore CD=\sqrt{CB^{2}-BD^{2}}=\sqrt{20^{2}-10^{2}}=\sqrt{300}=10\sqrt{3}$(km)，$AD = 90$km。在$Rt\triangle ACD$中，$AC^{2}=AD^{2}+CD^{2}=90^{2}+(10\sqrt{3})^{2}=8400$，$\therefore AC=\sqrt{8400}=20\sqrt{21}\approx20\times4.6 = 92$(km)。答：$A$、$C$之间的距离约为92 km。

 
(2)选择从$A$乘城际列车到$C$，再从$C$坐市内公共汽车到$B$。 理由如下： 由$A$到$B$所用的时间为$\frac{80}{60}=1\frac{1}{3}$(h)。 由$A$经$C$到$B$所用的时间为$\frac{92}{180}+\frac{20}{40}=1\frac{1}{90}$(h)。 $\because 1\frac{1}{90}＜1\frac{1}{3}$，$\therefore$选择从$A$乘城际列车到$C$再到$B$。