《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

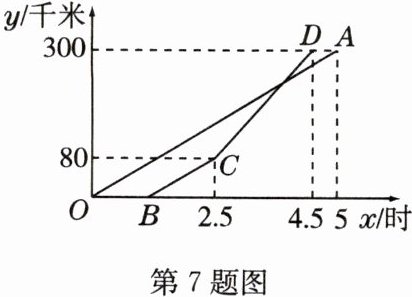
7 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地. 如图，线段$OA$表示货车离甲地距离$y$(千米)与时间$x$(时)之间的函数关系；折线$B - C - D$表示轿车离甲地距离$y$(千米)与时间$x$(时)之间的函数关系. 有下列说法：①货车的速度为60千米/时；②轿车与货车相遇时，货车恰好从甲地出发了3小时；③若轿车到达乙地后，马上沿原路以$CD$段速度返回，则轿车从乙地出发$\frac{3}{17}$小时后再次与货车相遇. 其中说法正确的是________.（填写序号）

答案： ①③ 解析：由题图可得，货车的速度为300÷5 = 60(千米/时)，故①正确。 设当2.5≤x≤4.5时，轿车对应的函数解析式为y = kx + b(k ≠ 0)， 则 \[ \begin{cases} 2.5k + b = 80 \\ 4.5k + b = 300 \end{cases} \] 解得 \[ \begin{cases} k = 110 \\ b = -195 \end{cases} \]
∴当2.5≤x≤4.5时，轿车对应的函数解析式为y = 110x - 195，易知货车对应的函数解析式为y = 60x，令110x - 195 = 60x，解得x = 3.9，即轿车与货车相遇时，货车恰好从甲地出发了3.9小时，故②错误。 若轿车到达乙地后，马上沿原路以CD段速度返回，设轿车从乙地出发t小时后再次与货车相遇，则60(4.5 + t) + \frac{300 - 80}{4.5 - 2.5}t = 300，解得t = \frac{3}{17}，故③正确。故答案为①③。

8（2022·齐齐哈尔）在一条笔直的公路上有$A、B$两地，甲、乙二人同时出发，甲从$A$地步行匀速前往$B$地，到达$B$地后，立刻以原速度沿原路返回$A$地. 乙从$B$地步行匀速前往$A$地(甲、乙二人到达$A$地后均停止运动)，甲、乙二人之间的距离$y$(米)与出发时间$x$(分)之间的函数关系如图所示，请结合图象解答下列问题：
（1）$A、B$两地之间的距离是________米，乙的步行速度是_______米/分；
（2）图中$a = $______，$b = $______，$c = $______；
（3）求线段$MN$的函数解析式；
（4）在乙运动的过程中，何时两人相距80米?（直接写出答案即可）

答案： 解：
(1)由函数图象可知，最开始时甲、乙两人之间的距离为1200米，
∵甲从A地出发，乙从B地出发，两人最开始时的距离就是A、B两地之间的距离，
∴A、B两地之间距离为1200米； 由图象可知乙经过20分钟到达A地，
∴乙的步行速度为\frac{1200}{20} = 60(米/分)。 故答案为1200，60。
(2)由函数图象可知，经过\frac{60}{7}分钟时两人相遇，经过c分钟时两人距离重新达到最大，此时甲到达B地，乙未到达A地，经过20分钟时乙到达A地，此时两人相距b米， 设甲的步行速度为x米/分，则\frac{60}{7}(x + 60) = 1200，解得x = 80，
∴c = \frac{1200}{80} = 15(分)，a = 15×60 = 900(米)， b = 1200 - (80×20 - 1200) = 800(米)。 故答案为900，800，15。
(3)由
(2)可知，点M，N的坐标分别为M(15,900)，N(20,800)， 设线段MN的解析式为y = kx + b(15≤x≤20)， 则有 \[ \begin{cases} 15k + b = 900 \\ 20k + b = 800 \end{cases} \] 解得 \[ \begin{cases} k = -20 \\ b = 1200 \end{cases} \]
∴线段MN的函数解析式是y = -20x + 1200(15≤x≤20)。
(4)设经过x分钟两人相距80米，两人相遇前和相遇后都可相距80米， 相遇前：1200 - (60 + 80)x = 80，解得x = 8， 相遇后：(60 + 80)x - 1200 = 80，解得x = \frac{64}{7}。
∴经过8分钟和\frac{64}{7}分钟时两人相距80米。

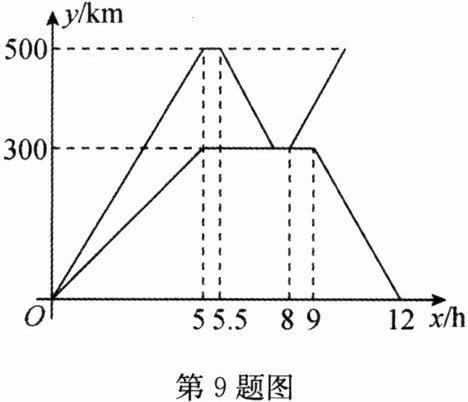
9（2022·龙东）为抗击疫情，支援$B$市，$A$市某蔬菜公司紧急调运两车蔬菜运往$B$市. 甲、乙两辆货车从$A$市出发前往$B$市，乙车行驶途中发生故障原地维修，此时甲车刚好到达$B$市. 甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往$B$市. 乙车维修完毕后立即返回$A$市. 两车离$A$市的距离$y$(km)与乙车所用时间$x$(h)之间的函数关系如图所示.
（1）甲车速度是________km/h，乙车出发时速度是________km/h.
（2）求乙车返回过程中，乙车离$A$市的距离$y$(km)与乙车所用时间$x$(h)的函数解析式(不要求写出自变量的取值范围).
（3）乙车出发多少小时时，两车之间的距离是120 km?请直接写出答案.

答案： 解：
(1)根据图象可得，甲车5 h行驶的路程为500 km，
∴甲车的速度为500÷5 = 100(km/h)； 乙车出发5 h行驶的路程为300 km，
∴乙车出发时的速度为300÷5 = 60(km/h)。 故答案为100，60。
(2)设y = kx + b(k ≠ 0)，由图象可得经过点(9,300)，(12,0)，
∴ \[ \begin{cases} 9k + b = 300 \\ 12k + b = 0 \end{cases} \] 解得 \[ \begin{cases} k = -100 \\ b = 1200 \end{cases} \]
∴所求函数解析式为y = -100x + 1200。
(3)设乙出发t时时，两车相距120 km， 根据图象可得，当0 ＜ t ＜ 5时， 100t - 60t = 120，解得t = 3； 当5 ＜ t ＜ 5.5时，根据图象可得不满足条件； 当5.5 ＜ t ＜ 8时， 500 - 100(t - 5.5) - 300 = 120，解得t = 6.3； 当8 ＜ t ＜ 9时，100(t - 8) = 120， 解得t = 9.2，不符合题意，舍去； 当9 ＜ t ＜ 12时， 100×(9 - 8) + 100(t - 9) + 100(t - 9) = 120， 解得t = 9.1。 综上可得，乙车出发3 h、6.3 h与9.1 h时，两车之间的距离为120 km。