第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
8 如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD和等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}=$______时,四边形ADFE为平行四边形.
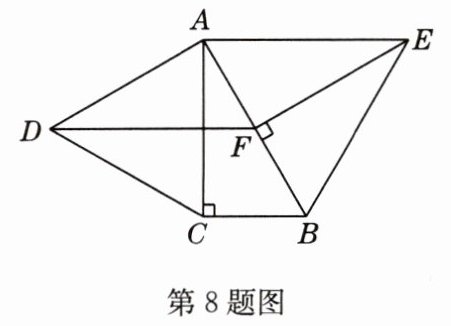

答案:
√3/2 解析:设AC = √3x,AB = 2x,
∴AD = AC = √3x. 在Rt△ABC中,
∵BC = √(AB² - AC²) = √((2x)² - (√3x)²) = √(4x² - 3x²) = √x² = x,
∴BC = 1/2 AB,
∴∠BAC = 30°.
∵△ACD为等边三角形,
∴∠DAC = 60°.
∴∠DAF = ∠EFA = 90°,
∴AD//EF. 在Rt△AEF中,AE = 2x,AF = 1/2 AB = x,
∴EF = AD = √3x,
∴当AC/AB = √3/2时,四边形ADFE为平行四边形.
∴AD = AC = √3x. 在Rt△ABC中,
∵BC = √(AB² - AC²) = √((2x)² - (√3x)²) = √(4x² - 3x²) = √x² = x,
∴BC = 1/2 AB,
∴∠BAC = 30°.
∵△ACD为等边三角形,
∴∠DAC = 60°.
∴∠DAF = ∠EFA = 90°,
∴AD//EF. 在Rt△AEF中,AE = 2x,AF = 1/2 AB = x,
∴EF = AD = √3x,
∴当AC/AB = √3/2时,四边形ADFE为平行四边形.
9 (2022·大庆)如图,在四边形ABDF中,点E,C为对角线BF上的两点,AB=DF,AC=DE,EB=CF. 连接AE,CD.
(1)求证:四边形ABDF是平行四边形;
(2)若AE=AC,求证:AB=DB.

(1)求证:四边形ABDF是平行四边形;
(2)若AE=AC,求证:AB=DB.

答案:
证明:
(1)
∵BE = CF,
∴BE + EC = EC + CF,
∴BC = EF,在△ABC和△DFE中,
∵{AB = DF, AC = DE, BC = FE},
∴△ABC≌△DFE(SSS),
∴∠ABC = ∠DFE,
∴AB//DF, 又
∵AB = DF,
∴四边形ABDF是平行四边形;
(2)由
(1)知,△ABC≌△DFE,
∴∠ACB = ∠DEF,AC = DE,
∵AE = AC,
∴∠AEC = ∠ACE = ∠DEF,AE = DE,
∴∠AEB = ∠DEB, 在△AEB和△DEB中,
∵{EB = EB, ∠AEB = ∠DEB, AE = DE},
∴△AEB≌△DEB(SAS),
∴AB = DB.
(1)
∵BE = CF,
∴BE + EC = EC + CF,
∴BC = EF,在△ABC和△DFE中,
∵{AB = DF, AC = DE, BC = FE},
∴△ABC≌△DFE(SSS),
∴∠ABC = ∠DFE,
∴AB//DF, 又
∵AB = DF,
∴四边形ABDF是平行四边形;
(2)由
(1)知,△ABC≌△DFE,
∴∠ACB = ∠DEF,AC = DE,
∵AE = AC,
∴∠AEC = ∠ACE = ∠DEF,AE = DE,
∴∠AEB = ∠DEB, 在△AEB和△DEB中,
∵{EB = EB, ∠AEB = ∠DEB, AE = DE},
∴△AEB≌△DEB(SAS),
∴AB = DB.
10 如图,D、E为等边△ABC的边AB、AC上的点且AE=BD,△BEF是以BE为一边的等边三角形. 求证:
(1)△AEB≌△BDC;
(2)四边形BFCD为平行四边形.
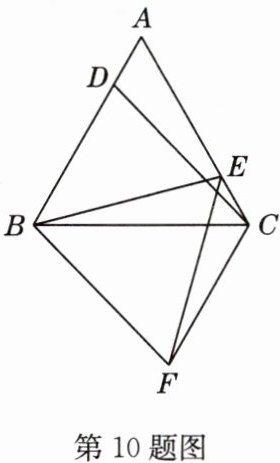
(1)△AEB≌△BDC;
(2)四边形BFCD为平行四边形.

答案:
证明:
(1)
∵△ABC为等边三角形,
∴∠A = ∠DBC,AB = BC. 又AE = BD,
∴△AEB≌△BDC.
(2)
∵△AEB≌△BDC,
∴BE = CD.
∵△BEF为等边三角形,
∴BF = BE,
∴BF = CD.
∵∠ADC = ∠ABC + ∠BCD = 60° + ∠BCD,∠ABF = ∠ABE + ∠EBF = 60° + ∠ABE. 又∠ABE = ∠BCD,
∴∠ADC = ∠ABF,
∴CD//BF.
∴四边形BFCD为平行四边形.
(1)
∵△ABC为等边三角形,
∴∠A = ∠DBC,AB = BC. 又AE = BD,
∴△AEB≌△BDC.
(2)
∵△AEB≌△BDC,
∴BE = CD.
∵△BEF为等边三角形,
∴BF = BE,
∴BF = CD.
∵∠ADC = ∠ABC + ∠BCD = 60° + ∠BCD,∠ABF = ∠ABE + ∠EBF = 60° + ∠ABE. 又∠ABE = ∠BCD,
∴∠ADC = ∠ABF,
∴CD//BF.
∴四边形BFCD为平行四边形.
11 (探究题)如图,已知点B为线段AD上一动点(不与端点重合). BC=AD,BC⊥AD,延长BC到点E,使得CE=BD,直线CD与直线AE相交于点P,它们的夹角∠APD是定值吗?请加以说明.
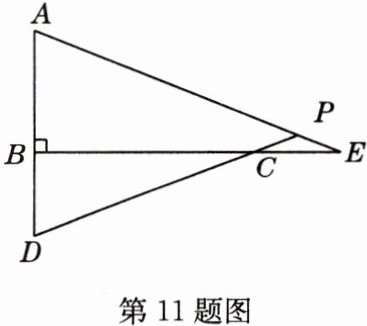

答案:
解:是定值. 作AF⊥AD,AF = CE. 连接FC,FD. 易证四边形AFCE是平行四边形.
∴CF//AE,
∴∠FCD = ∠APD. 易证△ADF≌△BCD,
∴FD = CD,∠ADF = ∠BCD. 又∠BCD + ∠BDC = 90°,
∴∠ADF + ∠BDC = 90°,
∴∠FDC = 90°,
∴∠FCD = 45°,
∴∠APD = ∠FCD = 45°.
∴CF//AE,
∴∠FCD = ∠APD. 易证△ADF≌△BCD,
∴FD = CD,∠ADF = ∠BCD. 又∠BCD + ∠BDC = 90°,
∴∠ADF + ∠BDC = 90°,
∴∠FDC = 90°,
∴∠FCD = 45°,
∴∠APD = ∠FCD = 45°.
12 △ABC是等边三角形,D是直线AB上的一点,∠CDM=60°,DM交直线AC于点M,作BN//CM,交直线DM于点N.
(1)如图,当点D在线段AB上时,线段AM与线段BD,BN之间有何数量关系?并说明理由.
(2)当点D在AB或BA的延长线上时,(1)中的关系是否发生变化?请选取其中一种情况进行证明.
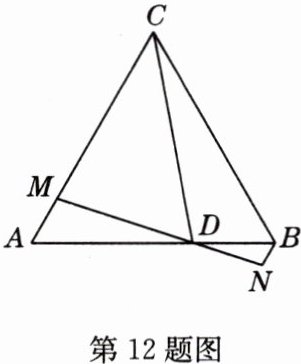
(1)如图,当点D在线段AB上时,线段AM与线段BD,BN之间有何数量关系?并说明理由.
(2)当点D在AB或BA的延长线上时,(1)中的关系是否发生变化?请选取其中一种情况进行证明.

答案:
解:
(1)AM与BD、BC之间的数量关系为AM = BD - BN. 理由:作NE//AB,交CA的延长线于点E. 又BN//CM,
∴四边形AENB为平行四边形,
∴AE = BN,EN = AB.
∵△ABC为等边三角形,
∴∠CAB = ∠CBA = 60°,AB = BC.
∵∠CDM = 60°,
∴∠CDB + ∠ADM = 120°.
∵∠CAB = 60°,
∴∠AMD + ∠ADM = 120°,
∴∠CDB = ∠NME. 又
∵∠E = ∠MAB = ∠DBC = 60°,EN = AB = BC,
∴△EMN≌△BDC,
∴EM = BD. 又EM = EA + AM = BN + AM,
∴AM = EM - BN = BD - BN.
(2)略.
(1)AM与BD、BC之间的数量关系为AM = BD - BN. 理由:作NE//AB,交CA的延长线于点E. 又BN//CM,
∴四边形AENB为平行四边形,
∴AE = BN,EN = AB.
∵△ABC为等边三角形,
∴∠CAB = ∠CBA = 60°,AB = BC.
∵∠CDM = 60°,
∴∠CDB + ∠ADM = 120°.
∵∠CAB = 60°,
∴∠AMD + ∠ADM = 120°,
∴∠CDB = ∠NME. 又
∵∠E = ∠MAB = ∠DBC = 60°,EN = AB = BC,
∴△EMN≌△BDC,
∴EM = BD. 又EM = EA + AM = BN + AM,
∴AM = EM - BN = BD - BN.
(2)略.
查看更多完整答案,请扫码查看


