《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 下列条件中，不能判定四边形ABCD是矩形的是（ ）
A. AB//CD，AD//BC，且∠A + ∠C = 180°
B. AB//CD，AD//BC，且∠A = ∠B
C. AB = CD，AD//BC，且∠A + ∠C = 180°
D. AB = CD，AD = BC，且∠A = ∠B

答案： C

2 矩形具有但平行四边形不一定具有的性质是（ ）
A. 对边相等
B. 对角相等
C. 对角线相等
D. 对角线互相平分

答案： C

3 如图，矩形ABCD的对角线AC、BD相交于点O，AE⊥BD于点E，且DE = OE，则∠ABD =（ ）

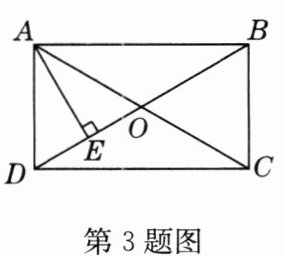
A. 20°
B. 30°
C. 45°
D. 不能确定

答案： B

4 如图，矩形ABCD中，AB = 5，BC = 3，点M为CD边上一点，且MA平分∠BMD，则DM的长是（ ）

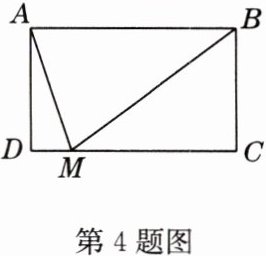
A. 0.5
B. 1
C. 1.5
D. 2

答案： B

5 (经典题)直角三角形斜边上的高和中线分别为5 cm和6 cm，则它的面积为（ ）
A. 30 cm²
B. 60 cm²
C. 45 cm²
D. 15 cm²

答案： A 解析：如图，在Rt△ABC中，∠ACB = 90°，CD是高，CE是中线，则AB = 2CE = 2×6 = 12(cm)。
∴S△ABC = $\frac{1}{2}$AB·CD = $\frac{1}{2}$×12×5 = 30(cm²)。![img id=1]

6 (2022·台州)如图，在△ABC中，∠ACB = 90°，D，E，F分别为AB，BC，CA的中点.若EF的长为10，则CD的长为______.

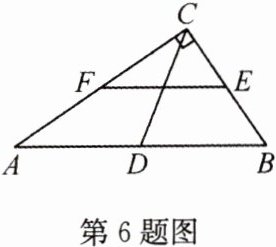
答案： 10 解析：
∵E，F分别为BC，AC的中点，
∴AB = 2EF = 20，
∵∠ACB = 90°，点D为AB的中点，
∴CD = $\frac{1}{2}$AB = 10，故答案为10。

7 (探究题)如图，∠MON = 90°，矩形ABCD的顶点A、B分别在边OM、ON上，当点B在ON上运动时，点A也随之在OM上运动.已知AB = 2，BC = 1，那么在运动过程中，点D到点O的最大距离为（ ）

A. $\sqrt{2}+1$
B. $\sqrt{5}$
C. $\frac{\sqrt{14 - 5}}{5}$
D. $\frac{5}{2}$

答案： A 解析：取AB的中点E，连接OE、DE，则DE = $\sqrt{DA^{2}+AE^{2}}$ = $\sqrt{1^{2}+1^{2}}$ = $\sqrt{2}$，OE = $\frac{1}{2}$AB = 1，当点O、E、D在同一条直线上时，点D到点O的距离最大，为$\sqrt{2}$ + 1。

8 如图，矩形ABCD中，点E在AD上，点F在AB上，EF⊥EC，且EF = EC，当DE = 2，矩形ABCD的周长为16时，AE的长是（ ）

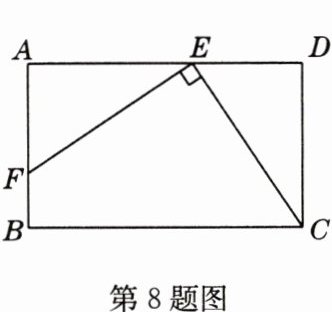
A. 3
B. 4
C. 5
D. 6

答案： A 解析：易证△AEF≌△DCE，
∴AF = DE = 2。设AE = CD = x。
∵矩形ABCD的周长为16，
∴AD + CD = 8，即x + 2 + x = 8，解得x = 3，
∴AE = 3。